Inventio
Vol. 20, núm. 51, 2024
doi: http://doi.org/inventio/10.30973/2024.20.51/8
Diseño de un instrumento para medir el dominio del álgebra
Design of an instrument to measure algebra dominance
Oscar Luis Ochoa Martínez
orcid: 0000-0003-3330-9138, chokar128@hotmail.com
Universidad Pedagógica de Durango (upd)
María Elena Rivera Heredia
orcid: 0000-0002-5835-0789, maelenarivera@gmail.com
Facultad de Psicología, Universidad Michoacana de San Nicolás de Hidalgo (umsnh)
resumen
El objetivo de este estudio consistió en diseñar un instrumento para medir el dominio del álgebra en estudiantes mexicanos en formación docente a nivel licenciatura. Participaron seis docentes expertos con perfil matemático en educación media superior, 79 estudiantes de la Licenciatura en Pedagogía y cinco jueces expertos en el manejo del álgebra en educación superior. Se inició con una versión de cincuenta ítems hasta lograr la versión final de treinta ítems, con un nivel aceptable en sus índices de dificultad y discriminación, buena fiabilidad y excelente validez de contenido. El instrumento cuenta con las características psicométricas necesarias para aplicarse en el campo de la investigación educativa.
palabras clave
educación matemática, evaluación del aprendizaje, habilidades cognitivas, psicometría
abstract
The objective of the study was to design an instrument to measure algebra proficiency of Mexican students in teacher training at the undergraduate level. Six expert teachers with a mathematical profile in higher middle education, 79 students of bachelor’s degree in pedagogy and five judges with expertise in the use of algebra in higher education participates. It started with a fifty items version until the final version of thirty items was achieved, the latter containing an acceptable level of difficulty and discrimination indices, good reliability and excellent content validity. The instrument has the necessary psychometric characteristics to be applied in the field of educational research.
key words
cognitive skills, learning assessment, mathematics education, psychometrics
Recepción: 06/04/24. Aceptación: 17/06/24. Publicación: 6/12/24.
Introducción
En la práctica educativa se reconoce la importancia que tiene el aprendizaje de las matemáticas por la utilidad que representa en el diario vivir del individuo, además de facilitar su desenvolvimiento en los diferentes niveles de estudio. Las dificultades en el pensamiento matemático, específicamente en el manejo del álgebra, son motivo frecuente de rezago y deserción escolar. Por situaciones como éstas, la formación del estudiante en el campo de la matemática es una preocupación en el ámbito educativo (Carreras García y Sivoli Barrios, 2020; Ramos Palacios et al., 2021).
En México, las dificultades en el aprendizaje y manejo del álgebra se reflejan en los resultados de pruebas internacionales, como el Programa para la Evaluación Internacional de los Estudiantes (pisa) (Márquez Jiménez, 2017), donde los puntajes de los alumnos mexicanos se encuentran por debajo de los de los estudiantes del resto de los países de la Organización para la Cooperación y Desarrollo Económico (ocde, 2019), incluyendo a los países latinoamericanos que forman parte de ésta, lo que confirma la necesidad de prestar mayor atención tanto a la enseñanza y medición como a la investigación sobre el álgebra en este país.
La problemática que representa el aprendizaje y manejo del álgebra es multifactorial, pero destacan las siguientes causas: el problema que representa la comprensión natural de las matemáticas; las habilidades cognitivas involucradas, entre ellas la capacidad de abstracción, cuya complejidad con frecuencia desalienta el interés por aprenderla y practicarla; el uso de técnicas e instrumentos inadecuados para su enseñanza y evaluación, así como la falta de innovación de los métodos de enseñanza del álgebra en el aula (García González et al., 2020; Vega Vega et al., 2015). Esta serie de dificultades ha provocado que, a través de la historia, el dominio del álgebra se haya constituido como un problema permanente que requiere atención constante (López y Bedolla, 2020).
Por otro lado, uno de los factores que han contribuido a mejorar el pensamiento matemático del estudiante en relación con el manejo del álgebra es el incremento en su evaluación, tanto en cantidad como en calidad, en los exámenes para el ingreso a las instituciones educativas, pues éstos cumplen una función crucial en la identificación de las competencias y dificultades que presentan los estudiantes (Retnawati et al., 2017).
Dada la importancia de los instrumentos de evaluación diagnóstica en las matemáticas y, por consiguiente, en el área del álgebra, se reconoce la existencia de este tipo de instrumentos, entre ellos los de opción múltiple; sin embargo, este tipo de instrumentos son una generalidad que, aun cuando muestran indicativos de confiablidad y validez, presentan dos inconvenientes:
- Tienen reactivos complicados, lo que puede originar errores en cuanto al dominio real que tiene el estudiante en el manejo del álgebra. Esta situación puede mejorarse con la integración de reactivos de dificultad media y alta discriminación, debido a que cuentan con un mayor coeficiente de predicción (De las Fuentes-Lara et al., 2022).
- La estructura de los ítems no es apropiada, lo que puede dificultar el diseño de una propuesta de mejora adecuada para facilitar al estudiante el aprendizaje del álgebra: “Una adecuada estructuración de los ítems establece la posibilidad de obtener información más exacta sobre el nivel de dominio de una determinada habilidad en el estudiante” (Moya Ricardo et al., 2016, p. 101).
En atención a esta problemática, se consideró conveniente construir y validar el instrumento de estudio con una muestra de 79 estudiantes de la Licenciatura en Pedagogía, ya que este programa tiene la característica de contar con alumnos con alto y pobre dominio del álgebra, debido a que en él convergen egresados de escuelas de educación media superior (ems) tanto con perfil de bachillerato técnico como del área de ciencias sociales y humanidades.
El estudio y aplicación del álgebra es parte esencial de la formación de estudiantes de educación superior (es) (Blandón Dávila, 2019), motivo por el cual se tomó la decisión de construir un instrumento de carácter diagnóstico, con el objetivo de medir el dominio del álgebra que, en determinado momento, pudieran tener los estudiantes en este nivel educativo. Para ello, se tomó como referencia la información contenida en el documento Formación y aprendizaje del álgebra (foraal) (García Moreno, 2019).
En este documento se plantea que en el dominio del álgebra coexisten las cinco dimensiones que se muestran en la tabla 1. A partir de éstas se construyeron los ítems que integran el Instrumento para Medir el Dominio del Álgebra (imda), objetivo de esta investigación.
Tabla 1
Dimensiones para el aprendizaje del álgebra
| Número de dimensión | Proceso al que corresponde |
|---|---|
| 1 | Paso de la aritmética al álgebra |
| 2 | Reversibilidad del pensamiento |
| 3 | Identificación de patrones |
| 4 | Generalización del conocimiento |
| 5 | La abstracción y la reflexión en los procesos matemáticos |
Fuente: elaborada con datos de García Moreno (2019).
Metodología
El estudio se considera de carácter instrumental, puesto que se enfoca en la elaboración de un instrumento de medición, así como en el análisis de sus propiedades psicométricas (Montero y León, 2007).
El proceso inicial de construcción del imda se realizó con base en las fases que exhibe el método Delphi, de acuerdo con la propuesta de López-Gómez (2018, p. 21) y con apoyo en las dimensiones indicadas en la tabla 1. Para tal efecto, se consideró el cumplimento de las siguientes cuatro etapas:
Etapa 1. Construcción de la primera versión del imda, con la participación de tres docentes expertos con perfil matemático en ems.
Etapa 2. Depuración de la primera versión del imda, con la participación de tres docentes expertos con perfil matemático en ems.
Etapa 3. Prueba piloto con la participación de 79 estudiantes de la Licenciatura en Pedagogía, la cual se realizó con el propósito de disminuir al máximo las deficiencias en la construcción y validación del imda, que pudieran surgir debido a la subjetividad de los criterios adoptados por los docentes expertos en la aplicación del método Delphi (García-Ruiz y Lena-Acebo, 2018). Este proceso incluyó las siguientes pruebas estadísticas:
- Medida de los índices de dificultad y discriminación de los ítems. Al margen de la utilidad e importancia del índice de dificultad, el índice de discriminación proporciona información sobre la calidad general de la prueba (Hurtado, 2018). Para su interpretación se siguió la clasificación propuesta por Gómez López et al. (2020), que puede apreciarse en la tabla 2.
- Medida de consistencia interna del instrumento o fiabilidad, la cual se determinó mediante el análisis estadístico de coeficiente Alfa 20 de Kuder-Richardson (Medina Paredes et al., 2019).
Etapa 4. Prueba de Validez de Contenido (cvc) del imda, la cual se determinó con el uso de la metodología expuesta por Hernández Nieto (2002). En este proceso participaron cinco jueces expertos con perfil matemático en es, quienes aportaron sus contribuciones en el formulario que se describe en la tabla 3.
Tabla 2
Clasificación e interpretación de los índices de dificultad y discriminación del imda
| Índice de dificultad | Índice de discriminación | Recomendación | ||
|---|---|---|---|---|
| Clasificación del ítem | Valor del índice | Clasificación del ítem | Valor del índice | |
| Fácil | 0.91-1 | Pésimo | < 0.01 | Descartar |
| Relativamente fácil | 0.81-0.90 | Pobre | 0 a 0.19 | Descartar o revisar |
| Dificultad adecuada | 0.51-0.80 | Regular | 0.20 a 0.29 | Revisar |
| Relativamente difícil | 0.40-0.50 | Buena | 0.30 a 0.39 | Con posibilidad de mejorar |
| Difícil | 0-0.39 | Excelente | 0.40 a 1 | Conservar |
Fuente: construcción personal con base en Gómez et al. (2020).
Tabla 3
Formulario para evaluar la segunda versión del imda con ejemplo de un item
| Formulario | |
|---|---|
| Evaluador | |
| Criterio | Indicadores |
| Coherencia | Identificación de patrones |
| Claridad | Generalización del conocimiento |
| Distractores | La abstracción y la reflexión en los procesos matemáticos |
| Relevancia | La abstracción y la reflexión en los procesos matemáticos |
| Escala de valores para la evaluación | |
| 1=Inaceptable 2=Deficiente 3=Regular 4=Bueno 5=Excelente | |
| Ítem 1 | En la expresión algebraica 8x + 8 = 0, ¿qué valor de “x” cumple con la condición de igualdad? |
| Opciones de respuesta | a) x=−4 b) x=8 c) x=−1 d) x=−2 |
Fuente: construcción personal.
Variables de respuesta
Los datos obtenidos en el estudio fueron organizados y clasificados con apoyo de Excel y analizados en el programa Statistical Package for Social Sciences (spss Statistics).
Resultados
Etapa 1. El producto del desarrollo de esta etapa fue la primera versión del imda conformada por cincuenta ítems.
Etapa2. La primera versión se depuró y el dictamen fue la eliminación de nueve ítems, de lo cual quedó una segunda versión del imda integrada por 41 ítems.
Etapa 3. Prueba piloto que incluyó las siguientes pruebas estadísticas:
- Medida de los índices de dificultad y discriminación.
Los 41 ítems seleccionados en la segunda versión fueron objeto de medida en sus índices de dificultad y discriminación. En la tabla 4 se observa el valor registrado en cada uno de ellos y, en función del rango de valores establecidos para su aceptación o rechazo descritos en la tabla 2, fueron eliminados los siete ítems señalados en negritas (R7, R8, R12, R27, R32, R34 y R35), de donde quedó una tercera versión integrada por 34 ítems. Al final de la tabla se localiza el valor de la media del estadístico del índice de dificultad (MIdif=0.68) e índice de discriminación (MIdisc=0.38).
Tabla 4
Índices de dificultad y discriminación del imda (segunda versión)
| No | ítem | Idif | Idisc | No | ítem | Idif | Idisc | No | ítem | Idif | Idisc | No | ítem | Idif | Idisc |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | R1 | 0.63 | 0.3 | 12 | R12 | 0.3 | 0.1 | 23 | R23 | 0.82 | 0.33 | 34 | R34 | 0.34 | 0.08 |
| 2 | R2 | 0.81 | 0.3 | 13 | R13 | 0.59 | 0.53 | 24 | R24 | 0.76 | 0.46 | 35 | R35 | 0.08 | -0.15 |
| 3 | R3 | 0.86 | 0.25 | 14 | R14 | 0.61 | 0.2 | 25 | R25 | 0.71 | 0.51 | 36 | R36 | 0.71 | 0.51 |
| 4 | R4 | 0.34 | 0.23 | 15 | R15 | 0.39 | 0.13 | 26 | R26 | 0.84 | 0.3 | 37 | R37 | 0.8 | 0.33 |
| 5 | R5 | 0.85 | 0.23 | 16 | R16 | 0.63 | 0.41 | 27 | R27 | 0.18 | -0.05 | 38 | R38 | 0.61 | 0.56 |
| 6 | R6 | 0.89 | 0.2 | 17 | R17 | 0.8 | 0.33 | 28 | R28 | 0.22 | 0.18 | 39 | R39 | 0.54 | 0.48 |
| 7 | R7 | 0.84 | 0.15 | 18 | R18 | 0.65 | 0.43 | 29 | R29 | 0.71 | 0.46 | 40 | R40 | 0.7 | 0.28 |
| 8 | R8 | 0.91 | 0.15 | 19 | R19 | 0.73 | 0.25 | 30 | R30 | 0.68 | 0.41 | 41 | R41 | 0.75 | 0.38 |
| 9 | R9 | 0.56 | 0.41 | 20 | R20 | 0.76 | 0.25 | 31 | R31 | 0.65 | 0.63 | MIdif = .68 MIdisc = .38 |
|||
| 10 | R10 | 0.66 | 0.25 | 21 | R21 | 0.62 | 0.63 | 32 | R32 | 0.44 | -0.18 | ||||
| 11 | R11 | 0.81 | 0.35 | 22 | R22 | 0.77 | 0.33 | 33 | R33 | 0.72 | 0.48 | ||||
Nota: Idif = Índice de dificultad; Idisc = Índice de discriminación.
Fuente: construcción personal.
Tabla 5
Datos para calcular el valor de los índices de dificultad y discriminación
| Reactivo 7 | ||||||||
| Opciones de respuesta | ||||||||
| Opción | A | B | C | D | Total | Aciertos (C) | I Dificultad | I Discriminación |
| Grupo alto (n=20) | 0 | 3 | 36 | 0 | 39 | 36 | 0.84 | 0.15 |
| Grupo bajo (n=20) | 6 | 1 | 30 | 3 | 40 | 30 | ||
| Total | 6 | 4 | 66 | 3 | 79 | |||
Fuente: construcción personal.
Tabla 6
Resultado de la prueba de fiabilidad
| Estadísticas de fiabilidad | |
| Alfa 20 de Kuder-Richardson | N de elementos |
| .89 | 41 |
Fuente: construcción personal.
Cálculo de los índices de dificultad y discriminación
La calidad de un reactivo de opción múltiple se da en función del valor de su índice de dificultad e índice de discriminación. Para determinar el cumplimiento de esta propiedad psicométrica de cada uno de los reactivos, se consideró como requisito permanecer dentro del siguiente intervalo de valores:

El cálculo del índice de dificultad se realizó con la siguiente fórmula:

El cálculo del índice de discriminación se realizó con la siguiente fórmula:
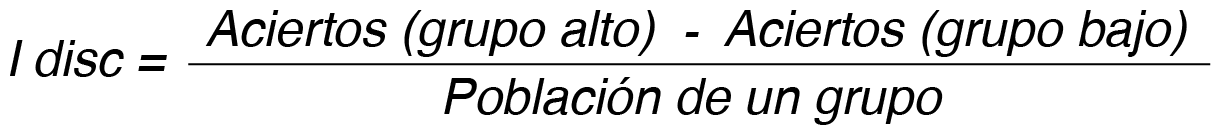
En la tabla 5 se encuentra la información necesaria para realizar el cálculo de ambos índices. En este caso se ejemplifica la evaluación del reactivo número 7, los datos correspondientes son los siguientes:
- Número de participantes en cada grupo (veinte participantes).
- Número de respuestas que contestaron los participantes de cada grupo en cada opción de respuesta.
- El total de aciertos que obtuvo cada grupo (para el caso, opción de respuesta “C”).
- Se aplican las fórmulas y se obtiene el valor de ambos índices.
- Los valores de ambos índices se cotejan con el intervalo de valores. Como resultado se obtuvo que ninguno se encuentra dentro del rango estipulado para ser considerado de buena calidad; por lo tanto, éste fue rechazado y eliminado del instrumento.
- Medida de fiabilidad
El resultado de esta prueba arrojó un estadístico del Alfa 20 de Kuder-Richardson con valor de 0.89. Este valor se considera como muy bueno y se encuentra en la tabla 6. La razón por la que se utilizó esta prueba se debe a que la respuesta al ítem es de tipo dicotómico y se realizó en consideración al valor medio del índice de dificultad del imda.
Etapa 4. Validez de contenido: En la tabla 7 (Anexo 1), se aprecia el valor del Coeficiente de Validez de Contenido de cada ítem (cvci), así como el valor del Coeficiente de Validez de Contenido total (cvct), este último con un valor (cvct = 0.93). De acuerdo con el criterio de interpretación indicado en el valor del estadístico, se considera como “excelente”.
En el resultado en esta medida ningún ítem obtuvo un coeficiente menor a 0.8; sin embargo, de acuerdo con observaciones realizadas por los jueces, fueron eliminados cuatro ítems que registraron la puntuación más baja. En esta condición, la versión final del imda quedó integrada por treinta ítems (Anexo 2), y cuenta con seis ítems en cada dimensión.
Conclusiones
Este trabajo es una continuación de la línea de investigación propuesta por las aportaciones de García Moreno (2019). Una aportación adicional del presente estudio fue la inclusión de estudiantes de es que se están formando en el campo de la pedagogía, espacio educativo en el que probablemente tengan que participar como docentes en la facilitación y aplicación de conceptos matemáticos con sus estudiantes (Cortés et al., 2016).
En este mismo sentido, los resultados de esta investigación contribuyen a ampliar y enriquecer el resultado de trabajos previos realizados sobre las diferentes áreas para la enseñanza y evaluación del conocimiento algebraico (Butto Zarzar et al., 2018; Larios et al. 2021; Reyes y Jaramillo, 2018; Valenzuela García y Gutiérrez Marfileño, 2018).
El trabajo de diseño del imda realizado por los docentes expertos con perfil matemático en ems, que transitó por la primera y segunda versión, se reforzó con la prueba piloto, de donde se obtuvo la tercera versión integrada por 34 ítems, la cual arrojó valores bastante aceptables en su índice de dificultad (MIdif = 0.68) e índice de discriminación (MIdisc = 0.38) (Gómez López et al., 2020; Medina Paredes et al., 2019). De acuerdo con los parámetros de medición establecidos, estos resultados indican la propiedad que tiene el imda para determinar el dominio real que tiene el estudiante en el álgebra. En este mismo sentido, la prueba de consistencia interna arrojó un coeficiente de fiabilidad de Kuder-Richardson (kr-20=0.89) con un valor bastante aceptable e indicativo de la precisión que tiene el imda para medir el dominio del álgebra en los estudiantes de es.
La versión final constituida por treinta ítems se definió con la prueba de validez de contenido (cvct = 0.93). Este valor del coeficiente se considera excelente e indicativo de una adecuada estructura de los ítems, además de confirmar la correspondencia que existe entre el rasgo del aprendizaje del evaluado y el contenido del imda.
El diseño del imda se considera importante porque atiende la problemática previamente citada, es decir, se valoró la complejidad y estructura de los ítems con el propósito de obtener un diagnóstico más cercano a la realidad, aspecto que concuerda con el tipo y las características de la muestra seleccionada.
Dadas las dificultades de los estudiantes mexicanos para el aprendizaje de las matemáticas (ocde, 2019), se espera que el producto de la presente investigación contribuya a mejorar las herramientas de evaluación con las que cuenta el país, ya que, a decir de Horbath y Gracia (2014), la medida de las habilidades y el pensamiento matemático son punto de partida para mejorar las prácticas de enseñanza y fortalecer las estrategias de aprendizaje en los estudiantes.
Referencias
Blandón Dávila, M. E. (2019). Propuesta metodológica para el proceso de enseñanzaaprendizaje del álgebra en primer año de la universidad. Revista Científica de farem-Estelí, 8(30), 20-27. https://doi.org/10.5377/farem.v0i30.7884
Butto Zarzar, C. M., Delgado Fernández, J. y Bazán Ramírez, A. (2018). Procesos de generalización: una vía de acceso al pensamiento algebraico temprano en educación básica. Horizontes Pedagógicos, 20(1), 25-36. https://doi.org/10.33881/0123-8264.hop.20104
Carreras García, F. de A. y Sivoli Barrios, Z. M. (2020). Diseño y validación de un instrumento para medir los conocimientos en matemáticas básicas que poseen los estudiantes de ciencia. Revista Ciencia Digital, 4(1), 253-269. https://doi.org/10.33262/cienciadigital.v4i1.1098
Cortés, J. C., Hitt, F. y Saboya, M. (2016). Pensamiento aritmético-algebraico a través de un espacio de trabajo matemático en un ambiente de papel, lápiz y tecnología en la escuela secundaria. Bolema: Boletim de Educação Matemática, 30(54), 240-264. http://dx.doi.org/10.1590/1980-4415v30n54a12
De las Fuentes-Lara, M., Aguilar-Salinas, W. E., Justo-López., A. C. e Iñiguez-Monroy, C. G. (2022). Medición de las habilidades algebraicas, trigonométricas y geométricas de los estudiantes en el curso de cálculo diferencial en ingeniería. Revista Española de Pedagogía, 80(282), 289-308. https://dialnet.unirioja.es/servlet/articulo?codigo=8438526
García González, M. del S., Cortés Ortega, J. y Rodríguez Vásquez, F. M. (2020). “Aprender matemáticas es resolver problemas”: creencias de estudiantes de bachillerato acerca de las matemáticas. Revista de Investigación Educativa de la Rediech, 11(e726), 1-17. http://dx.doi.org/10.33010/ie_rie_rediech.v11i20.726
García Moreno, M. D. C. (coord.) (2019). foraal. Formación y aprendizaje del álgebra. Red de Posgrados de Educación, ac. https://www.academia.edu/41613840/Formacion_y_aprendizaje_del_algebra
García-Ruiz, M. E. y Lena-Acebo F. J. (2018). Aplicación del método Delphi en el diseño de una investigación cuantitativa sobre el fenómeno fablab. empiria. Revista de Metodología de Ciencias Sociales, (40), 129-166. https://doi.org/10.5944/empiria.40.2018.22014
Gómez López, V. M., Rosales Gracia, S., García Galaviz, J. L., Berrones Sánchez, K. I., Berrones Sánchez, C. M. (2020). Índice de dificultad y discriminación de ítems para la evaluación en asignaturas básicas de medicina. Educación Médica Superior, 34(1). https://ems.sld.cu/index.php/ems/article/view/1727
Hernández Nieto, R. (2002). Contribuciones al análisis estadístico: sensibilidad (estabilidad y consistencia) de varios coeficientes de variabilidad relativa y el coeficiente de variación proporcional (cvp), el coeficiente de validez de contenido (cvc) y el coeficiente kappa, en la determinación de la validez de contenido según la técnica de juicio de expertos. Universidad de los Andes.
Horbath, J. E. y Gracia, A. (2014). Discriminación laboral y vulnerabilidad de las mujeres frente a la crisis mundial en México. Economía, Sociedad y Territorio, xiv(45), 465-495. https://www.redalyc.org/pdf/111/11130276005.pdf
Hurtado Mondoñedo, L. L. (2018). Relación entre los índices de dificultad y discriminación. Revista Digital de Investigación en Docencia Universitaria, 12(1), 273-300. http://dx.doi.org/10.19083/ridu.12.614
Larios Osorio, V., Spíndola Yáñez, P. I., Cuevas Salazar, O. y Castro, J. J. (2021). Conflictos semióticos y niveles de algebrización en aspirantes a Ingeniería. Educación Matemática, 33(3), https://doi.org/10.24844/EM3303.10
López, C. y Bedolla-Cornejo, L. P. (2020). El aprendizaje adaptativo para la regularización académica de estudiantes de nuevo ingreso: la experiencia en un curso remedial de matemáticas. edutec. Revista Electrónica de Tecnología Educativa, (74), 206-220. https://doi.org/10.21556/edutec.2020.74.1627
López-Gómez, E. (2018). El método Delphi en la investigación actual en educación: una revisión teórica y metodológica. Educación xx1, 21(1), 17-40. https://www.redalyc.org/articulo.oa?id=70653466002
Márquez Jiménez, A. (2017). A 15 años de pisa: resultados y polémicas. Revista Perfiles Educativos, xxxix(156), 3-15. https://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0185-26982017000200003
Medina Paredes, J. A., Ramírez Díaz, M. H. y Miranda, I. (2019). Validez y confiabilidad de un test en línea sobre los fenómenos de reflexión y refracción del sonido. Revista Apertura, 11(2), 104-121. http://dx.doi.org/10.32870/Ap.v11n2.1622
Montero, I. y León, O. G. (2007). A guide for naming research studies in psychology. International Journal of Clinical and Health Psychology, 7(3), 847-862. http://www.redalyc.org/articulo. oa?id=33770318
Moya Ricardo, D., Pérez Gómez, Y. y Ruiz, R. (2016). La Teoría de Respuesta al Ítem para la evaluación del aprendizaje en Matemática. EduSol, 16(55), 91-102. https://dialnet.unirioja.es/servlet/articulo?codigo=5678501
Organización para la Cooperación y Desarrollo Económico (2019). pisa 2018 Results. What school life means for students’ lives. Volume iii. ocde. https://doi.org/10.1787/acd78851-en
Ramos Palacios, L. A., Guifarro, M. I. y Casas García, L. M. (2021). Dificultades en el aprendizaje del álgebra, un estudio con pruebas estandarizadas. Boletim de Educação Matemática, 35(79), 1016-1033. https://doi.org/10.1590/1980-4415v35n70a21
Reyes, A. y Jaramillo, J. (2018). Propiedades de simetría y reversibilidad para álgebras cuánticas y extensiones torcidas de Poincaré-Birkhoff-Witt Extensions. Ingeniería y Ciencia, 14(27), 29-52. https://doi.org/10.17230/ingciencia.14.27.2
Retnawati, H., Kartowagiran, B., Arlinwibowo, J. y Sulistyaningsih, E. (2017). Why are the mathematics national examination items difficult and what is teachers’ strategy to overcome it? International Journal of Instruction, 10(3), 257-276. https://doi.org/10.12973/iji.2017.10317a
Valenzuela García, J. y Gutiérrez Marfileño, V. E. (2018). Desarrollo del pensamiento algebraico en estudiantes de bachillerato a través de la generalización visual de sucesiones de figuras. Educación Matemática, 30(2), 49-72. https://doi.org/10.24844/EM3002.03
Vega Vega, J. C., Niño Duarte, F. y Cárdenas, Y. P. (2015). Enseñanza de las matemáticas básicas en un entorno e-Learning: un estudio de caso de la Universidad Manuela Beltrán Virtual. Revista Escuela de Administración de Negocios, 79, 172-185. https://journal.universidadean.edu.co/index.php/Revista/article/view/1274
Anexo 1 (tabla 7)
Cálculo del cvct del imda
| Ítem | ΣXi | Mxi | cvci | Pei | cvci |
| 1 | 91 | 4.55 | 0.91 | 0.00032 | 0.90968 |
| 2 | 91 | 4.55 | 0.91 | 0.00032 | 0.90968 |
| 3 | 96 | 4.80 | 0.96 | 0.00032 | 0.95968 |
| 4 | 92 | 4.60 | 0.92 | 0.00032 | 0.91968 |
| 5 | 86 | 4.30 | 0.86 | 0.00032 | 0.85968 |
| 6 | 94 | 4.70 | 0.94 | 0.00032 | 0.93968 |
| 7 | 89 | 4.45 | 0.89 | 0.00032 | 0.88968 |
| 8 | 93 | 4.65 | 0.93 | 0.00032 | 0.92968 |
| 9 | 93 | 4.65 | 0.93 | 0.00032 | 0.92968 |
| 10 | 93 | 4.65 | 0.93 | 0.00032 | 0.92968 |
| 11 | 96 | 4.80 | 0.96 | 0.00032 | 0.95968 |
| 12 | 93 | 4.65 | 0.93 | 0.00032 | 0.92968 |
| 13 | 97 | 4.85 | 0.97 | 0.00032 | 0.96968 |
| 14 | 95 | 4.75 | 0.95 | 0.00032 | 0.94968 |
| 15 | 96 | 4.58 | 0.96 | 0.00032 | 0.95968 |
| 16 | 92 | 4.60 | 0.92 | 0.00032 | 0.91968 |
| 17 | 86 | 4.30 | 0.86 | 0.00032 | 0.85968 |
| 18 | 96 | 4.80 | 0.96 | 0.00032 | 0.95968 |
| 19 | 93 | 4.65 | 0.93 | 0.00032 | 0.92968 |
| 20 | 93 | 4.65 | 0.93 | 0.00032 | 0.92968 |
| 21 | 90 | 4.50 | 0.90 | 0.00032 | 0.89968 |
| 22 | 92 | 4.60 | 0.92 | 0.00032 | 0.91968 |
| 23 | 99 | 4.95 | 0.99 | 0.00032 | 0.98968 |
| 24 | 94 | 4.70 | 0.94 | 0.00032 | 0.93968 |
| 25 | 97 | 4.85 | 0.97 | 0.00032 | 0.96968 |
| 26 | 97 | 4.85 | 0.97 | 0.00032 | 0.96968 |
| 27 | 92 | 4.60 | 0.92 | 0.00032 | 0.91968 |
| 28 | 95 | 4.75 | 0.95 | 0.00032 | 0.94968 |
| 29 | 99 | 4.95 | 0.99 | 0.00032 | 0.98968 |
| 30 | 93 | 4.65 | 0.93 | 0.00032 | 0.92968 |
| cvct | 0.93401 | ||||
Nota: Coeficiente de Validez de Contenido de cada ítem (cvci); Coeficiente de Validez de Contenido total (cvct).
Anexo 2
Instrumento para medir el dominio del álgebra imda
