Inventio
Vol. 20, núm. 52, 2024
doi: https://doi.org/10.30973/inventio/2024.20.52/1
Números metálicos, un vínculo entre matemáticas y estética
Metallic numbers, a link between mathematics and aesthetics
Leonardo Di Girolamo Sigalotti Díaz
orcid: 0000-0001-8043-0825, leonardo.sigalotti@gmail.com
Área de Física de Procesos Irreversibles, Departamento de Ciencias Básicas, Universidad Autónoma Metropolitana (uam), Unidad Azcapotzalco
Otto Rendón
orcid: 0000-0002-3708-6560, ottorendon@gmail.com
Departamento de Ciencias Básicas, Universidad Autónoma Metropolitana (uam), Unidad Azcapotzalco
resumen
Los números metálicos son números irracionales en cuanto sus expresiones decimales están conformadas por cifras infinitas que se siguen sin repetir un patrón fijo. El número metálico más celebrado es el llamado número de oro o razón áurea, el cual se encuentra frecuentemente en la naturaleza y que, además, aparece muchas veces en diferentes áreas, incluyendo las matemáticas, la geometría, la física, la arquitectura, el arte, entre otras. Sin embargo, junto al número de oro existe toda una familia de otros números metálicos menos conocidos, como la razón de plata, de bronce, etcétera, que, al igual que la razón áurea, pueden construirse como la razón entre los lados de un segmento o de un rectángulo.
palabras clave
números irracionales, números notables, razones metálicas, sucesión numérica
abstract
Metallic numbers are irrational numbers as their decimal expressions are made up of infinite figures that follow each other without repeating a fixed pattern. The most celebrated metallic number is the so-called golden number, or golden ratio, which is frequently found in nature and appears many times in different areas, including mathematics, geometry, physics, architecture and art, among others. However, along with the golden number there is a whole family of other less known metallic numbers, such as the silver ratio, the bronze ratio, etc., which, like the golden ratio, can be constructed as the ratio between the sides of a segment or a rectangle.
key words
irrational numbers, notable numbers, metallic ratios, numerical sequence
Recepción: 18/03/24. Aceptación: 03/07/24. Publicación: 18/02/25.
Introducción
La aparición del número de oro o razón áurea —también conocida como proporción divina o sección áurea, como fue bautizada originalmente por Leonardo da Vinci (1452-1519), en latín sectio aurea—, en la naturaleza como en muchas áreas del conocimiento, no sólo ha despertado mucho interés en este número a lo largo de los años, sino que también ha sido objeto de publicaciones en libros (Livio, 2002; Meisner, 2018) y artículos (Falbo, 2005; Fett, 2006; Kak, 2010), así como de innumerables comentarios y reseñas divulgativas en internet.
En general, el número de oro es denotado por la letra griega φ (Phi), notación propuesta en 1900 por el ingeniero eléctrico, físico e inventor estadounidense Mark Barr, en honor al escultor y arquitecto griego Fidias, quien diseñó el Partenón, el famoso templo dedicado a la diosa Atenea. Este número ha sido un indicador de la perfección, por su relación con las proporciones armoniosas que guardan algunos edificios, modelos estéticos y objetos cotidianos, desde el famoso Hombre de Vitruvio dibujado por Leonardo da Vinci en 1492 hasta las tarjetas de crédito. En su obra Elementos, Euclides lo llamó “media y extrema razón”.
El número de oro fue lanzado a la luz como objeto de atención particular por el monje italiano Luca Pacioli en su obra De Divina Proportione, si bien ahí no se le atribuía alguna propiedad estética. Como ocurre en la vida, el número de oro ha tenido tanto entusiastas como detractores. Estos últimos lo han catalogado con frecuencia como una constante matemática marginal sin conexión con las composiciones geométricas, como bien lo expresó en una nota periodística el economista y matemático español Juan José R. Calaza (2010). Sin embargo, por su conexión con la estética y el arte se le considera una constante universal relacionada con la perfección y la cultura.
Los famosos números de oro y plata
En particular, el número de oro se encuentra definido por la célebre expresión
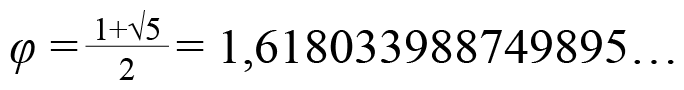 (1)
(1)
Si bien mucha de la atención brindada a este número desde la antigüedad se debe a la influencia de la escuela pitagórica, en tiempos recientes se sigue descubriendo su presencia en áreas de la física, como la termodinámica (Huleihl, 2012; Popkov y Shipitsyn, 2000) y la relatividad especial (Sigalotti y Mejias, 2006), e inclusive en otras áreas, como el análisis y la predicción de los movimientos bursátiles.
En una serie de artículos, el ingeniero y físico egipcio M. S. El Naschie introdujo la idea de que el espacio-tiempo a pequeñas escalas espaciales es fractal y cuya dimensión de Hausdorff es igual a 4+φ3 = (1/φ)3 = 4.236067977…, donde φ = (√5-1)/2 = 0.618033988749895… corresponde a la dimensión de Hausdorff de un conjunto de Cantor aleatorio (El Naschie, 2005).
Por fractal se entiende un objeto geométrico cuya estructura, la cual puede ser fragmentada o irregular, se repite a escalas espaciales siempre más pequeñas. Dichos objetos geométricos poseen dimensiones no enteras, es decir, fraccionarias y a esas dimensiones se les llama dimensiones de Hausdorff. La dimensión de Hausdorff de un conjunto de Cantor estándar es ln2/ln3 ≈ 0.630929754…, mientras que un conjunto de Cantor aleatorio se refiere a un subconjunto de Cantor del intervalo [0,1], construido siguiendo el método de construcción recursiva aleatoria introducido por Mauldin y Williams (1986) y cuya dimensión de Hausdorff es φ.
Como se podrá observar en lo que sigue, φ es la solución de una ecuación algebraica de segundo grado y, por lo tanto, admite dos valores distintos: φ(1) = (1+√5)/2 ≈ 1.618033988… y φ(2) = (1-√5)/2 ≈ - 0.618033988…, que cumplen con la propiedad φ(1) = -1/φ(2). En efecto, la dimensión de Hausdorff de un conjunto de Cantor construido aleatoriamente está dada por la relación φ = -φ(2) = 1/φ(1). Basado en la razón áurea, la teoría propuesta por El Naschie (2004) predice que las masas de las partículas elementales del modelo estándar pueden expresarse en términos de φ con sorprendente exactitud.
El número de oro también aparece frecuentemente en la distribución de las ramas de un árbol o planta, de las hojas y, más aún, de las semillas. Recordemos que una de las revelaciones más notorias de este número en la naturaleza es la famosísima concha del nautilo (Nautilus pompilius), que posee la forma de la espiral áurea, construida a partir de una serie de rectángulos áureos. Se dice que un rectángulo es áureo si la razón entre su lado mayor y su lado menor es exactamente igual a φ.
En la serie infinita de números metálicos, el número de oro es seguido por otro número especial, también conocido en la antigüedad y llamado número de plata, o simplemente razón plateada, el cual es denotado comúnmente por la letra griega δ y definido por la expresión
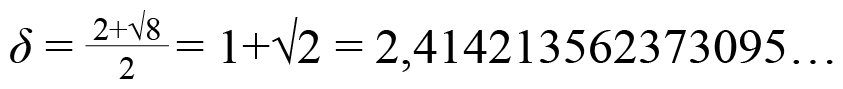 (2)
(2)
Si bien menos famoso que el número de oro, este número debe su notoriedad, desde tiempos antiguos, a la relación con la raíz cuadrada de dos y a su conexión con el octágono regular, en alusión a la bien conocida conexión existente entre la razón áurea (1) y el pentágono regular (figura 1). Mientras el número de oro puede definirse también como la limitante del cociente entre dos números consecutivos de la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55…), el número de plata es la limitante del cociente entre dos números consecutivos de la sucesión de Pell (1, 2, 5, 12, 29, 70, 169, 408…).
Figura 1
(a) Número de oro en el pentágono regular unitario y (b) número de plata en el octágono regular unitario
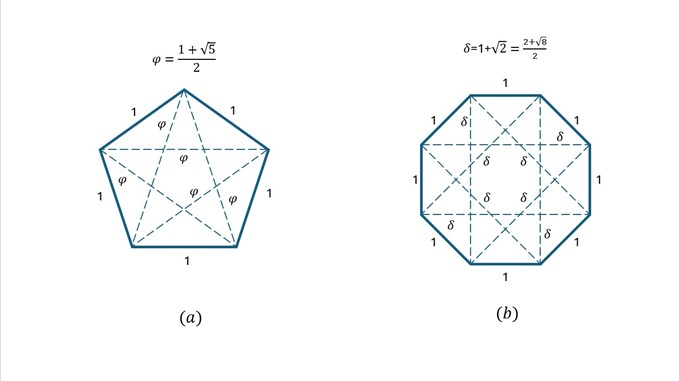
El pentágono regular de lados unitarios posee cinco lados diagonales iguales al número de oro, mientras el octágono regular de lados unitarios posee ocho lados diagonales iguales al número de plata.
Fuente: elaboración propia.
Es importante recordar que el sistema de proporciones en la antigua Roma se encontraba basado en la sección plateada y sus aproximaciones enteras. En efecto, evidencias claras del uso de la razón plateada se encontraron principalmente en las ruinas de la ciudad romana de Ostia, donde casas y edificios diseñados por arquitectos del siglo ii d. C. se encontraban en proporción del número de plata y de sus potencias sucesivas.
Familia de números metálicos
La familia completa de números metálicos se puede visualizar como la solución positiva de la ecuación algebraica de segundo grado
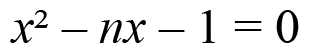
que es de la forma
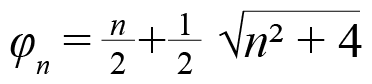 (3)
(3)
donde n = 1, 2, 3,… Es fácil demostrar que todos los números metálicos satisfacen la bien conocida identidad φn – n = 1/φn. Además, la serie de números metálicos también puede expresarse en términos de fracciones continuas puras (Rittaud, 2006), esto es:
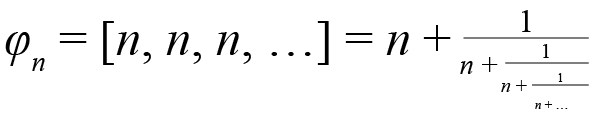 (4)
(4)
El conjunto de números metálicos fue introducido en 1994 por la matemática argentina Vera W. de Spinadel, quien comentó que tales números aparecían con frecuencia en el diseño de las construcciones romanas (Spinadel, 1998). Para n = 1, las expresiones (3) y (4) conducen a la razón áurea (1), mientras que n=2 corresponde a la razón plateada (2), φ2 = δ.
Observando la expresión (4), el número de oro es aquel que posee los cocientes parciales más pequeños (es decir, iguales a 1). Sin embargo, como lo explica Rittaud (2006), a éste le sigue la raíz cuadrada de 2, que obedece a una fracción continua con el primer cociente igual a 1 y el resto de los cocientes iguales a 2, lo cual resulta evidente del vínculo existente entre la raíz de 2 y el número de plata. A los números de oro y plata les siguen otros menos preponderantes como, por ejemplo, el número de bronce para n = 3, el número de cobre para n = 4, y así sucesivamente.
Habiendo ya descrito los dos más importantes, la tabla 1 muestra los números metálicos que siguen hasta n = 9.
Figura 2
Gráfico que muestra cómo calcular la n-ésima razón metálica a partir de la partición de un segmento de línea
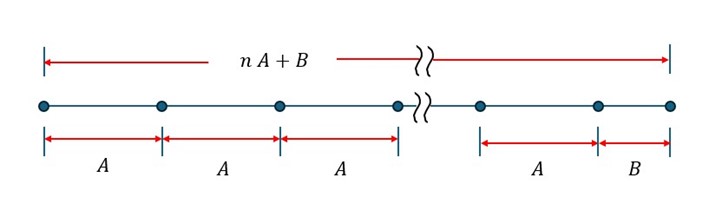
División de un segmento de línea en n segmentos de longitud A y un segmento de longitud B para la derivación general de las proporciones metálicas.
Fuente: elaboración propia.
Tabla 1
Números metálicos desde n = 3 hasta n = 9
| Nombre | n | Fórmula | Representación decimal |
|---|---|---|---|
| Bronce | 3 | (3+√13)⁄2 | 3.30277563773199… |
| Cobre | 4 | (4+√20)⁄2 | 4.23606797749979… |
| Níquel | 5 | (5+√29)⁄2 | 5.19258240356725… |
| Aluminio | 6 | (6+√40)⁄2 | 6.16227766016838… |
| Hierro | 7 | (7+√53)⁄2 | 7.14005494464025… |
| Estaño | 8 | (8+√68)⁄2 | 8.12310562561766… |
| Plomo | 9 | (9+√85)⁄2 | 9.10977222864644… |
Fuente: datos tomados de Rosetta Code (2025).
Desde el punto de vista de la geometría
Geométricamente, la forma más simple para derivar las proporciones metálicas es dividir un segmento de longitud l en n + 1 partes, es decir, n partes de longitud A y una parte de longitud B con A > B, como se muestra en la figura 2, de manera que la razón entre una de las secciones de mayor longitud, A, y la de menor longitud, B, es igual a la razón entre la longitud total del segmento, l = nA+B, y la longitud de la sección de mayor longitud, A, es decir:
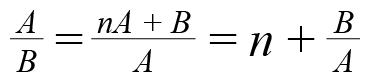 (5)
(5)
Si A y B son simples números, diremos entonces que se encuentran en proporción metálica si se cumple la relación (5). Haciendo x = A/B, es fácil demostrar que la relación (5) es equivalente a la ecuación algebraica x2 – nx – 1 = 0, cuya solución positiva está dada por la relación (3). Si bien los números metálicos se encuentran definidos para valores enteros positivos n ≥ 1, a veces es frecuente encontrar la solución positiva x = 1 para n = 0, que corresponde a un caso degenerado.
En algunas partes muy puntuales de la literatura se refiere a este número como el número de platino. Sin embargo, en matemáticas se acostumbra definir el número de platino como la solución positiva de la ecuación cuadrática x2 – 2x – 2 = 0, cuyo valor exacto es 1 + √3. Los nombres de metales asignados a los números más allá del número de plata no siguen una correspondencia o regla lógica, más bien corresponden a asignaciones fantasiosas. Por ejemplo, Rajput (2021) llama a la secuencia de números metálicos con n ≥ 3 secuencia de números de bronce.
Figura 3
(a) Rectángulo áureo, (b) de plata y (c) de bronce, construidos a partir de cuadrados unitarios
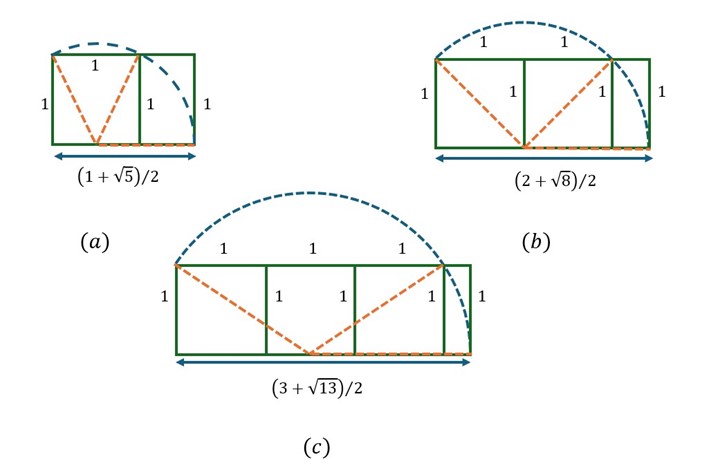
La longitud de la base en (a) corresponde exactamente al número de oro, en (b) al número de plata y en (c) al número de bronce.
Fuente: elaboración propia.
En el numerador de la razón áurea, la raíz de 5 aparece acompañada de 1 de manera que se requiere el uso de un solo cuadrado unitario, mientras las raíces de 8 y de 13 en los numeradores de los números de plata y bronce están acompañadas de 2 y de 3, por lo que se requiere la unión de dos y tres cuadrados unitarios, respectivamente.
Existen muchas otras formas geométricas para derivar las proporciones metálicas. Entre las más conocidas están aquellas que hacen recurso de cuadrados unitarios y rectángulos. Por ejemplo, el número de oro puede construirse a partir de un cuadrado unitario. Haciendo centro con un compás en el punto medio de la base del cuadrado y trazando un arco de círculo que una los dos vértices superiores del cuadrado e intercepte la prolongación de la base, se obtiene un rectángulo de proporción áurea, como se muestra en la figura 3(a).
Partiendo ahora de la unión de dos cuadrados unitarios para obtener un rectángulo de altura 1 y base igual a 2, centrando el compás en el punto medio de la base y trazando un arco de círculo que una los dos vértices superiores del rectángulo e intercepte la prolongación de la base, se obtiene un rectángulo con las proporciones del número de plata, como se puede apreciar de la figura 3(b). Siguiendo procedimientos similares y partiendo de la unión de tres cuadrados unitarios, se puede llegar al número de bronce (figura 3[c]). Para conformar el n-ésimo número metálico, se seguirá el mismo procedimiento anterior, partiendo de la unión de n cuadrados unitarios.
Notas finales
En este artículo de carácter divulgativo se ha hecho un esfuerzo por recoger algunos aspectos fundamentales de la familia de los números metálicos, con el propósito de despertar el interés del lector en este fascinante mundo de los números irracionales extremos y de su incidencia en la naturaleza y en diferentes áreas del conocimiento humano. Sin embargo, es importante mencionar que el aporte en este artículo es limitado, en la medida en que las aplicaciones del número de oro y sus familiares son tan numerosas que sería imposible condensar dicha información en un solo artículo.
En la antigüedad se pensaba que los elementos arquitectónicos expresaban mayor belleza, equilibrio y armonía si se ajustaban a la proporción áurea. Por esta razón, el número de oro se encuentra presente en una multitud de obras de arte como, por ejemplo, esculturas y objetos varios. Hoy en día esta forma de percepción de la belleza y la armonía sigue intacta, con el aliciente de que las proporciones metálicas siguen apareciendo en diferentes áreas de la ciencia y la ingeniería.
Referencias
Calaza, J. J. R. (27 de junio de 2010). El mito del número de oro. El Faro de Vigo . https://www.farodevigo.es/opinion/2010/06/27/mito-numero-oro-17833587.html
El Naschie, M. S. (2004). A review of E-infinity theory and the mass spectrum of high energy particle physics. Chaos, Solitons & Fractals, 19(1), 209-236. https://doi.org/10.1016/S0960-0779(03)00278-9
El Naschie, M. S. (2005). A guide to the mathematics of E-infinity Cantorian spacetime theory. Chaos, Solitons & Fractals, 25(5), 955-964. https://doi.org/10.1016/j.chaos.2004.12.033
Falbo, C. (2005). The golden ratio: a contrary viewpoint. The College Mathematics Journal, 36(2), 123-134. https://doi.org/10.2307/30044835
Fett, B. (2006). An in-depth investigation of the divine ratio. The Mathematics Enthusiast, 3(2), 157-175. https://doi.org/10.54870/1551-3440.1047
Huleihl, M. (2012). Golden section heat engines and heat pumps. Latin-American Journal of Physics Education, 6(3), 368-374. http://www.lajpe.org/sep12/07_LAJPE_680_Mahmud_Hleihil_preprint_corr_f.pdf
Kak, S. (2010). The golden mean and the physics of aesthetics. En B. Yadav y M. Mohan (eds.), Ancient indian leaps into mathematics (pp. 111-119). Birkhäuser. https://doi.org/10.1007/978-0-8176-4695-0_7
Livio, M. (2002). The golden ratio: the story of phi, the world’s most astonishing number. Broadway Books.
Mauldin, R. D. y Williams S. C. (1986). Random recursive constructions: asymptotic geometric and topological properties. Transactions of the American Mathematical Society, 295(1), 325-346. https://doi.org/10.2307/2000159
Meisner, G. B. (2018). The golden ratio: the divine beauty of mathematics. Race Point Publishing. https://doi.org/10.2307/30044835
Popkov, V. V. y Shipitsyn, E. V. (2000). Golden section in the Carnot cycle. Physics-Uspekhi,
Rajput, C. (2021). Metallic ratios: beyond the golden mean ratio. The mathematical relationship between different metallic means. Journal of Advances in Mathematics, 20, 158-166. https://doi.org/10.24297/jam.v20i.9023
Rittaud, B. (2006). Le fabuleux destin de √2. Editions Le Pommier. https://doi.org/10.2307/30044835
Rosetta Code (14 de enero de 2025). Metallic Ratios. Rosetta Code, sp. https://rosettacode.org/wiki/Metallic_ratios
Sigalotti, L. Di G. y Mejias, A. (2006). The golden ratio in special relativity. Chaos, Solitons & Fractals, 30(3), 521-524. https://doi.org/10.1016/j.chaos.2006.03.005
Spinadel, V. W. de (1998). From the Golden Mean to Chaos. Nueva Librerías.