Artificial intelligence applied to solar collectors for the heating of water for domestic use
Wassila Ajbar
orcid: 0000-0002-2107-3044/wassila.ajbar@gmail.com
Centro de Investigación en Ingeniería y Ciencias Aplicadas (ciicap), Universidad Autonama del Estado de Morelos (uaem)
José Alfredo Hernández Pérez
orcid: 0000-0003-3406-3758/alfredo@uaem.mx
Centro de Investigación en Ingeniería y Ciencias Aplicadas (ciicap), Universidad Autónoma del Estado de Morelos (uaem)
Arianna Parrales Bahena
orcid: 0000-0001-8554-8777/arianna.parrales@uaem.mx
Centro de Investigación en Ingeniería y Ciencias Aplicadas (ciicap), Universidad Autónoma del Estado de Morelos (uaem)
Armando Huicochea
orcid: 0000-0002-4067-0143/huico_chea@uaem.mx
Centro de Investigación en Ingeniería y Ciencias Aplicadas (ciicap), Universidad Autónoma del Estado de Morelos (uaem)
David Juárez-Romero
orcid: 0000-0003-0942-9738/djuarezr7@uaem.mx
Centro de Investigación en Ingeniería y Ciencias Aplicadas (ciicap), Universidad Autónoma del Estado de Morelos (uaem)
resumen
La mayoría de los investigadores ha promovido el uso de energías renovables para reducir los combustibles fósiles. El sol es la fuente renovable más limpia. Una forma de aprovecharla es a través de colectores solares de canal parabólico ccp. En este trabajo se muestra el desarrollo de dos modelos de simulación matemática para predecir la temperatura de salida de un sistema ccp mediante la aplicación de la técnica de la inteligencia artificial que calienta agua. Los modelos mostraron resultados satisfactorios, al permitir controlar el proceso de manera eficaz e inteligente. La metodología desarrollada muestra el potencial de ser implementada en otros sistemas energéticos para predecir sus patrones.
abstract
Most researchers have promoted the use of renewable energies to reduce fossil fuels. The sun is the cleanest renewable source. One way to harness it is through parabolic solar collectors ptc. This paper shows the development of two mathematical simulation models to predict the output temperature of a ptc system by applying the artificial intelligence water heating technique. The models showed satisfactory results, allowing to control the process in an efficient and intelligent way. The developed methodology shows the potential to be implemented in other energy systems to predict their patterns.
palabras clave
inteligencia artificial, colectores solares térmicos, energías renovables, simulación matemática
key words
artificial intelligence, thermal solar colectors, renewable energies, mathematics simulations
Introducción
Para reducir las consecuencias ambientales por el consumo de energía proveniente de combustibles fósiles, la mayoría de los países y sus investigadores han promovido el uso de energías renovables. Dentro de las fuentes de energía consideradas renovables, la energía solar es la más limpia, con alto potencial y como una posible alternativa sostenible que podría satisfacer la demanda energética mundial, teniendo en cuenta que necesita ser captada y almacenada de manera eficiente. Una forma de aprovechar la energía del sol es a través de los colectores solares térmicos (Behar et al., 2013), de los cuales existen varios tipos, dependiendo de su aplicación y diseño.
Los colectores solares térmicos (cst) son un tipo particular de intercambiadores de calor que se utilizan para absorber la radiación solar entrante, transformarla en calor y luego transferirla a un fluido de trabajo. Algunas de sus aplicaciones más frecuentes son la generación de calor para tratamiento de agua (desalinización), la calefacción de agua doméstica, la calefacción y refrigeración de espacios, la cocción mediante hornos solares, la refrigeración, el calor de suministro para procesos industriales (pasteurización, secado, esterilización), entre otros (Evangelisti et al., 2019; Maurer et al., 2017).
Antecedentes
Los colectores solares térmicos se clasifican principalmente en dos tipos, según la relación de concentración: concentrados y no concentrados. Dentro de la clasificación de los colectores solares de concentración, el colector solar de canal parabólico (ccp) destaca por su amplio ángulo de aceptación y alta capacidad para aprovechar la luz difusa. La figura 1 muestra el ejemplo de un sistema ccp para el calentamiento de agua de uso doméstico.
Figura 1
Sistema de los colectores solares de canal parabólico para el calentamiento de agua de uso doméstico
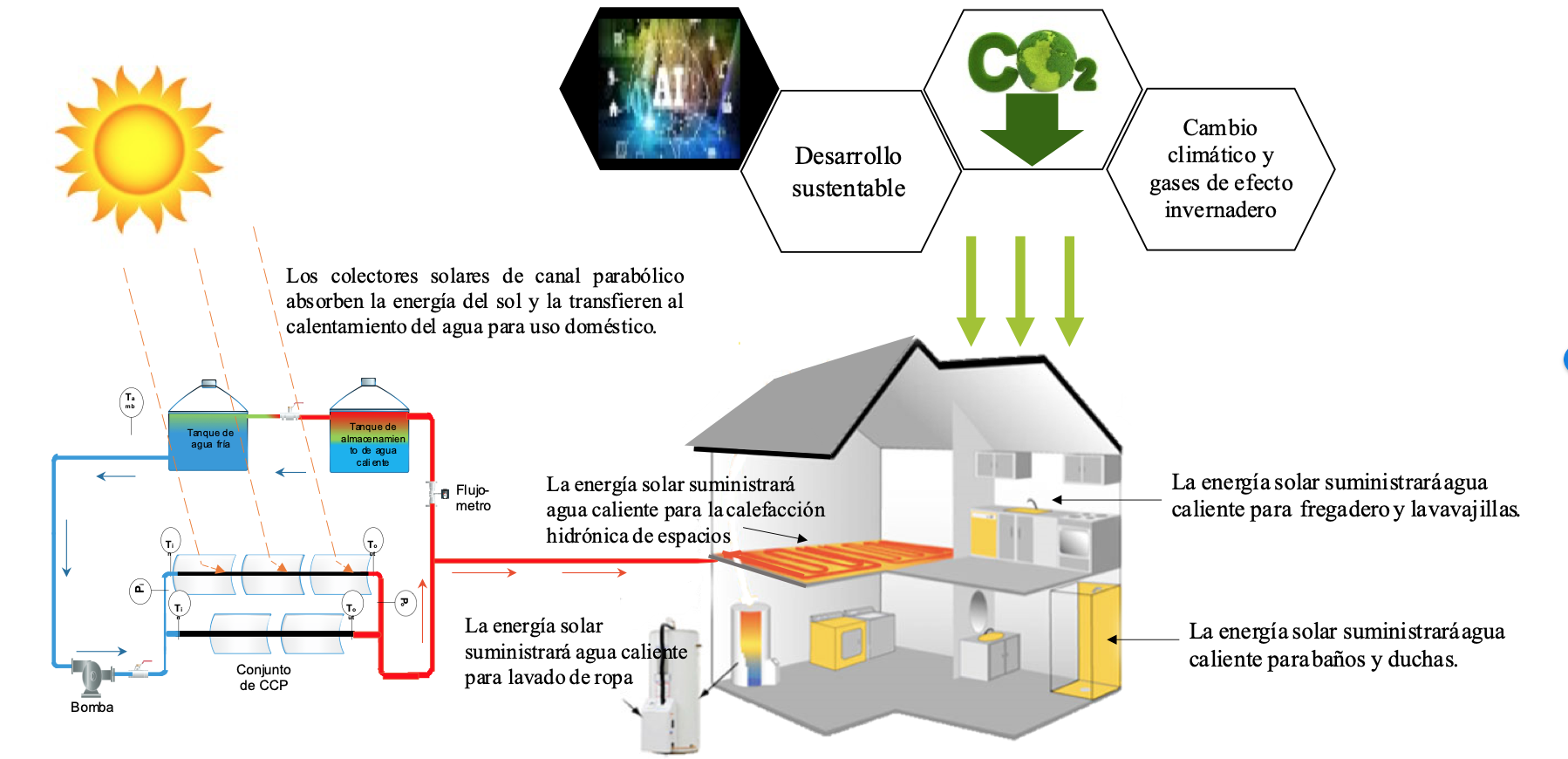
Fuente:Elaboración propia
Los ccp tienen un amplio intervalo de disponibilidad térmica que permite cumplir con los requerimientos de energía de algunos procesos industriales o de generación de energía eléctrica, además de ser rentable y amigable con el medio ambiente (Fathabadi, 2020). Tienen un costo razonable de unos 275 €/m2 (Cocco y Cau, 2015) y una eficiencia óptima media anual del 60% (Kincaid et al., 2018). Hoy en día, se sabe que su implementación en procesos industriales puede reducir una cantidad muy significativa de emisiones de CO2 por año con tan sólo 250 a 400 kg/m2 de superficie del colector (Jaber et al., 2004).
El ccp utiliza un reflector parabólico para concentrar los rayos solares incidentes a lo largo de una línea focal en la que se coloca un tubo absorbente. Su función principal es transformar la radiación solar y convertirla en energía térmica aumentando la temperatura de un fluido de transferencia de calor (ftc), el cual circula en el tubo absorbedor. Los ftc pueden ser agua, aceite térmico, aire o sal fundida (Bellos et al., 2016; Zarza Moya., 2016). Luego, la energía térmica recolectada se almacena o se utiliza en algunos procesos. Generalmente, el tubo absorbedor tiene un recubrimiento selectivo para disminuir la emitancia y reducir las pérdidas térmicas.
Estos sistemas deben colocarse con orientación e-o o n-s dependiendo la latitud de la región de su instalación para, con ello, tener menores pérdidas. Además, se recomienda instalarlo en áreas abundantes en sol debido a la ganancia neta de calor anual, la cual es cuatro veces mayor que la obtenida en un área promedio para un mismo sistema. Si se le incorpora un sistema de seguimiento solar, la energía solar absorbida en la superficie móvil es aproximadamente 46.46% más alta que la de la superficie fija (Bakos, 2006).
En lo que respecta a la eficiencia térmica del sistema ccp, numerosas investigaciones se han centrado en comprender cómo los diferentes parámetros de funcionamiento afectan la cantidad absorbida de radiación solar concentrada dentro del receptor. Sin embargo, los estudios experimentales están limitados por requerir un alto costo operativo y tiempo. Por consiguiente, se han inclinado hacia el uso de modelos matemáticos empíricos para describir el fenómeno con alta precisión y con ello reemplazar algunos experimentos (Reyes-Téllez et al., 2020).
Una de las alternativas más utilizadas actualmente en el modelado matemático empírico de este fenómeno no lineal ha sido la inteligencia artificial (ia) (Fadaei et al., 2018). Las técnicas de ia ofrecen una solución objetiva y reproducible a los problemas complejos no lineales donde no es posible encontrar una solución analítica. Específicamente, los datos provenientes de sistemas ccp son buenos candidatos para ser manejados con estas técnicas, ya que es difícil identificar una función matemática con descripción física precisa cuando algunos parámetros varían con el tiempo y factores ambientales
La ia se define como la capacidad de imitar la inteligencia humana en los movimientos de comprensión, percepción, resolución de problemas y toma de decisiones. Está basada en el aprendizaje de prueba y error de los fenómenos involucrados sin previo conocimiento físico, lo cual la hace atractiva para describir procesos complejos. Las redes neuronales artificiales (rna) son un subtipo de ia que se originó en la literatura informática y se inspiran precisamente en el aprendizaje humano. Con los avances en la ia y las ciencias de la computación, las rna pueden aprender a resolver problemas complejos en un tiempo muy razonable y se han convertido en una gran alternativa para identificar patrones de comportamiento.
Las rna constan de múltiples capas que contienen elementos denominados neuronas, las cuales están conectadas en paralelo y organizadas en tres capas: una capa de entrada, una o más capas ocultas y una capa de salida. La conexión entre las neuronas de las distintas capas se asocia con valores de ponderación llamados pesos y valores de compensación llamados bias, los cuales permiten el aprendizaje (Demuth et al., 2015).
El interés de las rna reside principalmente en las conexiones interneuronales y en la transmisión de información que se realiza entre ellas. Como se sabe biológicamente, cuando la neurona es estimulada a través de sus dendritas se produce un cambio en el potencial eléctrico. A veces el potencial no es suficiente para llevar la neurona al umbral, pero se puede sumar con otros para desencadenar un potencial de acción y transformarse transitoriamente en una señal numérica. Este comportamiento de señalización dinámica representa un factor clave en el procesamiento eficiente de la información.
En las conexiones neuronales artificiales, la neurona calcula su grado de conectividad mediante la función de activación o función de transferencia, que representa la tasa potencial a la que la neurona se activa o no. Existen diferentes tipos de funciones de transferencia o activación, por ejemplo: funciones escalonadas, lineales, sigmoidales logarítmicas, sigmoidales, gaussianas e inversas gaussianas. Las más destacadas son, para la capa oculta, la función tangencial sigmoidal (tansig) y la logarítmica sigmoidal (logsig). Normalmente se utiliza una función de transferencia lineal (purelin) para la capa de salida. Sin embargo, cabe mencionar que nuestro grupo de trabajo desarrolló nuevas funciones de transferencia basadas en cálculos fraccionados (Solís-Pérez et al., 2022), por ejemplo, las conformables funciones de transferencia. Hasta el momento están siendo evaluadas las nuevas funciones y se están comportando con excelentes resultados.
Cuando se lleva a cabo el entrenamiento de las rna es fundamental utilizar la normalización (o estandarización) de los datos para ajustar a la misma escala. Este proceso permite comparar sus proporciones en lugar de sus magnitudes. El intervalo de normalización de las variables debe estar relacionado con la función de activación que se decida utilizar. Por lo general, se realiza en intervalos de -1 a 1, para lo cual existen diferentes ecuaciones en la literatura (Reyes-Téllez et al., 2020).
Para evaluar el desempeño de los modelos de tna los resultados numéricos obtenidos deben validarse mediante análisis estadístico. Lo anterior incluye el cálculo del error cuadrático medio (ecm), el error porcentual absoluto medio (epam) y el coeficiente de determinación (r2). Los detalles de este análisis se pueden consultar en la publicación de Ajbar et al. (2021).
Metodología
El Grupo de Investigación en Ingeniería y Modelado de Procesos Térmicos, Mecánicos y Ambientales del Centro de Investigación en Ingeniería y Ciencias Aplicadas (ciicap) de la Universidad Autónoma del Estado de Morelos (uaem) ha desarrollado estudios numéricos y validación experimental de un sistema ccp para calentamiento de agua de uso doméstico aplicando ia (Ajbar et al., 2021). Este estudio consistió en el desarrollo de un modelo de red neuronal capaz de predecir la temperatura de salida en un sistema de colectores solares parabólicos de bajo costo, los cuales utilizan agua como fluido de trabajo.
La base de datos experimentales fue resultado de diferentes pruebas que se llevaron a cabo con variaciones de flujos volumétricos y temperaturas de entrada y tiempo (meses). Como se puede observar en la figura 2, el sistema experimental estuvo compuesto por colectores solares con diferentes ángulos de apertura y longitudes. Fue instrumentado con termopares tipo T debidamente calibrados para la medición de temperatura en las regiones de interés y un piranómetro para la medición de la radiación solar, así como la dirección y velocidad del viento. El tanque de alimentación y almacenamiento cuenta con resistencias eléctricas para que el sistema ccp pueda ser alimentado con el fluido a distintas temperaturas de entrada.
En el estudio se utilizó una tarjeta de adquisición de datos Agilent Technologies 34970IA, con tarjeta multiplexora HP34901A y una computadora personal para el registro de las temperaturas, flujo volumétrico, velocidad del viento, radiación solar, entre otros parámetros. Es importante mencionar que, una vez que fue alcanzada la temperatura deseada en el tanque de almacenamiento térmico, se abrió la válvula por arriba del tanque y se purgaron los ccp, es decir, se disminuyó la cantidad del fluido de calentamiento para evitar el problema del sobrecalentamiento. El sistema de colectores fue de pequeña escala y estuvo diseñado para operar a diversas temperaturas sin cambio de fase en el fluido de trabajo.
Figura 2
Esquema del ciclo del sistema experimental diseñado
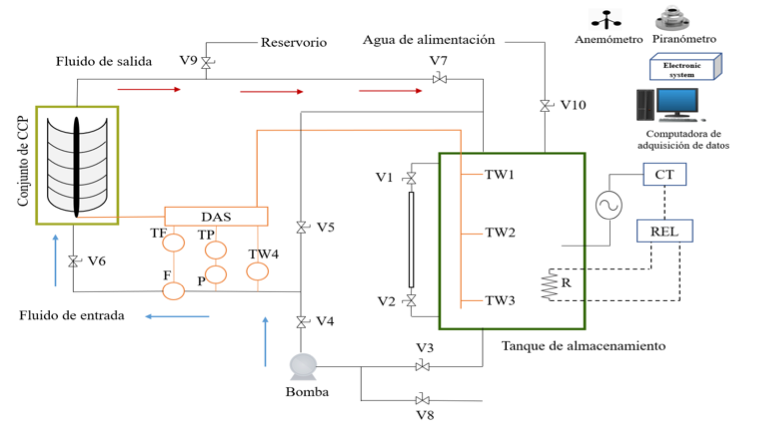
Fuente: elaboración propia.
Para llevar a cabo el entrenamiento, los datos experimentales fueron normalizados entre 0.1 y 0.9. Posteriormente, se dividieron en subconjuntos aleatorios de 60% para entrenamiento, 20% para validación y el resto para pruebas. El ángulo de borde (ángulo entre el eje y una línea desde el foco hasta el borde físico del concentrador), la temperatura de entrada del fluido, la temperatura del medio ambiente, el flujo volumétrico, la radiación del sol y la velocidad del viento fueron las variables consideradas para la capa de entrada del modelo de red neuronal artificia
El algoritmo de aprendizaje de pesos y bias utilizados en la formulación del modelo fue Levenberg-Marquardt (lm), considerando las dos funciones de transferencia logsig y tansig en la capa oculta y la función lineal purelin en la capa de salida. Además, ya evaluamos las funciones conformables de transferencia. Con la finalidad de encontrar el mejor modelo de simulación, cada modelo se entrenó en un intervalo de 1 a 4 neuronas en la capa oculta para predecir la temperatura de salida del sistema. Posteriormente, se realizaron análisis estadísticos y la prueba de pendiente intercepto para cada modelo, con la finalidad de determinar el número de neuronas ocultas y la función de transferencia óptimos.
Resultados y discusión
De acuerdo con los resultados obtenidos, los cuales se muestran en las tablas 1 y 2, se puede observar que, a medida que aumenta el número de neuronas en la capa oculta, el rendimiento del modelo mejora representando adecuadamente el patrón de comportamiento del fenómeno. Sin embargo, se debe considerar un valor máximo para evitar un sobreentrenamiento (tabla 1 y tabla 2).
Tabla 1
Resultados de la red neuronal artificial utilizando la función tansig en la capa oculta
| Arquitectura ann |
ecm |
r2 |
r |
mape % |
Ecuación de línea de regresión |
| 6-1-1 |
2.9178 |
0.9768 |
0.9883 |
3.6942 |
Tout,simulada = 0.9766 Tout,exp + 1.5216 |
| 6-2-1 |
0.7709 |
0.9984 |
0.9992 |
0.904 |
Tout,simulada = 0.9982 Tout,exp + 0.1134 |
| 6-3-1 |
0.7707 |
0.9984 |
0.9992 |
0.903 |
Tout,simulada = 0.9982 Tout,exp + 0.1158 |
| 6-4-1 |
0.6242 |
0.9989 |
0.9995 |
0.781 |
Tout,simulada = 0.9987 Tout,exp+ 0.0833 |
Tabla 2
Resultados de la red neuronal artificial utilizando la función losing en la capa oculta
| Arquitectura ann |
ecm |
r2 |
r |
mape % |
Ecuación de línea de regresión |
| 6-1-1 |
2.9178 |
0.9768 |
0.9883 |
3.6942 |
Tout,simulada = 0.9766 Tout,exp + 1.5215 |
| 6-2-1 |
0.7708 |
0.9984 |
0.9992 |
0.9038 |
Tout,simulada = 0.9982 Tout,exp + 0.1138 |
| 6-3-1 |
0.5820 |
0.9991 |
0.9995 |
0.6799 |
Tout,simulada = 0.9990 Tout,exp + 0.0648 |
| 6-4-1 |
0.6293 |
0.9989 |
0.9995 |
0.6784 |
Tout,simulada = 0.9988 Tout,exp + 0.0774 |
Donde ecm es el error cuadrático medio, r2 es el coeficiente de determinación y r es el coeficiente de correlación.
El mejor ajuste de los datos de entrenamiento se obtuvo con dos modelos (indicado en negritas en las tablas 1 y 2). El primero tuvo una arquitectura 6-2-1, considerando una función de transferencia logsig en la capa oculta. El coeficiente de determinación r2 obtenido fue de 0.9984, con un ecm de 0.7708, mientras que el segundo modelo tuvo una arquitectura 6-3-
1 con la función de transferencia tansig en la capa oculta. El coeficiente de determinación r2 obtenido fue de 0.9984 con un ecm de 0.7707.
La figura 3 muestra que, al realizar la comparación de los resultados numéricos de ambos modelos con los datos experimentales, se puede observar un notable grado de correlación, lo que pone de manifiesto su efectividad en la predicción del comportamiento térmico a la salida del sistema ccp.
Figura 3
Correlación entre la temperatura de salida del CCP experimental y predicha por el modelo de redes neuronales artificial
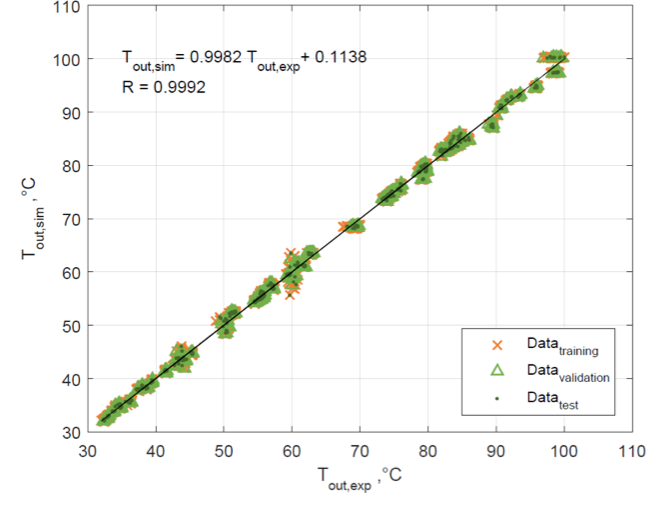
Fuente: elaboración propia.
Cabe subrayar que este tipo de modelos matemáticos obtenidos, basados en redes neuronales
artificiales, son utilizados para controlar las variables de operación de ccp con la finalidad de operar el sistema de manera óptima en línea y de forma inteligente. Lo anterior permite trabajar el proceso de manera energéticamente renovable y con la menor pérdida de transferencia de energía. Por consiguiente, aplicar las técnicas de ia permite controlar el proceso energético de una manera eficaz e inteligente.
Conclusiones
El uso de la inteligencia artificial ha demostrado ser una herramienta computacional poderosa y precisa para obtener modelos de predicción de fenómenos no lineales, como lo es el comportamiento termodinámico a la salida de los colectores solares. Con este estudio se demostró la eficacia, simplicidad y rapidez de los modelos obtenidos para la predicción de la temperatura de salida del sistema ccp. Esto nos lleva a resaltar que la ia es la herramienta más precisa y con mayor poder que existe hoy en día para la predicción de patrones. Además, nos permite ahorrar energía y operar el sistema experimental de los ccp de forma óptima.
Referencias
Ajbar, W., Parrales, A., Silva-Martínez, S., Bassam, A., Jaramillo, O. A. y Hernández, J. A. (2021). Identification of the Relevant Input Variables for Predicting the Parabolic Trough Solar Collector’s Outlet Temperature Using an Artificial Neural Network and a Multiple Linear Regression Model. Journal of Renewable and Sustainable Energy, 13(4), 043701. https://doi.org/10.1063/5.0055992
Bakos, G. C. (2006). Design and construction of a two-axis Sun tracking system for parabolic trough collector (ptc) efficiency improvement. Renewable Energy, 31(15), 2411-2421.https://doi.org/10.1016/j.renene.2005.11.008
Behar, O., Khellaf, A. y Mohammedi, K. (2013). Design and construction of a two-axis Sun tracking system for parabolic trough collector (ptc) efficiency improvement. A review of studies on central receiver solar thermal power plants. Renewable and Sustainable Energy Reviews, 23(1), 12-39. https://doi.org/10.1016/j.rser.2013.02.017
Bellos, E., Tzivanidis, C., Antonopoulos, K. A. y Gkinis, G. (2016). Thermal enhancement of solar parabolic trough collectors by using nanofluids and converging-diverging absorber tube. Renewable Energy, 94, 213-222. https://doi.org/10.1016/j.renene.2016.03.062
Cocco, D. y Cau, G. (2015). Energy and economic analysis of concentrating solar power plants based on parabolic trough and linear Fresnel collectors. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 229(6), 677-88. https://doi.org/10.1177/0957650915587433
Demuth, H. B., Beale, M. H. y Hagan, M. T. (2015). Neural Network Toolbox Reference. MathWorks.
Evangelisti, L., De Lieto V., R. y Asdrubali, F. (2019). Latest advances on solar thermal collectors: A comprehensive review. Renewable and Sustainable Energy Reviews, 114, 109318. https://doi.org/10.1016/j.rser.2019.109318
Fadaei, N., Yan, W., Tafarroj, M. M. y Kasaeian, A. (2018). The application of artificial neural networks to predict the performance of solar chimney filled with phase change materials. Energy, Conversion and Management, 171, 1255-1262. https://doi.org/10.1016/j.enconman.2018.06.055
Fathabadi, H. (2020).Novel low-cost parabolic trough solar collector with tpct heat pipe and solar tracker: Performance and comparing with commercial flat-plate and evacuated tube solar collectors. Solar Energy, 195, 210-222. https://doi.org/10.1016/j.solener.2019.11.057
Jaber, J., Badran, O. O. y Abu-Shikhah, N. (2004). Sustainable energy and environmental impact: Role of renewables as clean and secure source of energy for the 21st century in Jordan. Singapore Journal of Tropical Geography, 6(1), 174-186. https://doi.org/10.1007/s10098-003-0232-9
Kincaid, N., Mungas, G., Kramer, N., Wagner, M. y Zhu, G. (2018). An optical performance comparison of three concentrating solar power collector designs in linear Fresnel, parabolic trough, and central receiver. Applied Energy, 231(1), 1109-1121.https://doi.org/10.1016/j.apenergy.2018.09.153
Maurer, C., Cappel, C. y Kuhn, T. E. (2017). Progress in building-integrated solar thermal systems. Solar Energy, 154, 158-186.https://doi.org/10.1016/j.solener.2017.05.065
Reyes-Téllez, E. D., Parrales, A., Ramírez-Ramos, G. E., Hernández, J. A., Urquiza, G., Heredia, M. I., Sierra, F. Z. (2020). Analysis of transfer functions and normalizations in an ann model that predicts the transport of energy in a parabolic trough solar collector. Desalination and Water Treatment, 200, 223-41. https://doi.org/10.5004/dwt.2020.26063
Solís-Pérez, J. E., Hernández, J. A., Parrales, A., Gómez-Aguilar, J. F., Huicochea, A. (2022). Artificial neural networks with conformable transfer function for improving the performance in thermal and environmental processes. Neural Networks, 152, 44-56. https://doi.org/10.1016/j.neunet.2022.04.016
Zarza Moya, E. (2017). Innovative working fluids for parabolic trough collectors. En: Manuel J. Blanco, M. J. y L. Ramirez Santigosa (2017), Advances in Concentrating Solar Thermal Research and Technology (pp. 75-106). Woodhead Publishing. Woodhead Publishing Series in Energy. https://doi.org/10.1016/B978-0-08-100516-3.00005-8


