Vol. 18, núm. 45, 2022
http://doi.org/10.30973/inventio/2022.18.45/3
Quiralidad biológica: la asimetría funcional de la vida
Biological chirality: the functional asymmetry of life
Hugo Iván Cruz Rosas María Eugenia Noble Terán José Manuel Cruz Thomas Buhse La quiralidad es una propiedad geométrica en objetos que existen en dos versiones orientadas en el espacio a manera de reflejo. El caso típico son las manos, pues el reflejo de la mano izquierda da como resultado una mano derecha, y viceversa. En química, las reacciones que generan compuestos quirales lo hacen en cantidades equivalentes de moléculas izquierdas y derechas. En los sistemas vivos, durante la síntesis de proteínas la maquinaria celular sólo usa aminoácidos izquierdos, mientras que las principales rutas metabólicas favorecen el uso de carbohidratos derechos. En este escrito abordamos el concepto de quiralidad y mostramos la evidencia para considerarla una propiedad que optimiza el flujo de información en sistemas vivos. Chirality is a geometric property in objects that exist in two versions oriented in space as a reflection. The typical case is the hands, since the reflection of the left hand results in a right hand, and vice versa. In chemistry, reactions that generate chiral compounds do so in equivalent amounts of left and right molecules. In living systems, during protein synthesis, the cellular machinery only uses left amino acids, while the main metabolic pathways favor the use of right carbohydrates. In this paper we address the concept of chirality and show the evidence to consider it a characteristic that optimizes the flow of information in living systems. quiralidad, información biológica, dogma central de la biología molecular, sistemas dinámicos chirality, biological information, main tenet of molecular biology, dynamical systems Un objeto es quiral si no puede hacerse coincidir con su imagen en el espejo por medio de rotaciones o traslaciones. Esta es la definición de quiralidad actualmente aceptada, propuesta por Vladimir Prelog en 1975 en su lectura al recibir el Premio Nobel de Química. Empero, la primera vez que se definió el término fue en 1893, por el físico William Thompson (Lord Kelvin) con motivo de una conferencia en el Club Juvenil de Ciencias de la Universidad de Oxford. La palabra quiral se usó para enfatizar el componente geométrico, pues proviene del vocablo griego χєιρ (jir o quir), que significa “mano” (figura 1). En términos de Lord Kelvin: Llamo quiral a una figura geométrica o conjunto de puntos, y digo que posee quiralidad, si su imagen en un espejo plano, idealmente realizada, no puede hacerse coincidir con ella misma (citado en Cronin y Reisse, 2005). Sin embargo, la historia de la quiralidad se rastrea hasta mediados del siglo xix en Europa. Si bien ya existía una serie de observaciones y teorías, como la ley de la conservación de la masa en las reacciones químicas (enunciada por Antoine Lavoisier en 1789) o el modelo atómico y las mediciones de algunos pesos de éstos (publicados por John Dalton en 1805), que forman parte del desarrollo de la teoría atómica moderna y que convergieron para dar paso al concepto actual de quiralidad, es en la persona de Louis Pasteur en quien recae el mérito del descubrimiento de lo que hoy llamamos quiralidad molecular. La publicación en 1848 de los resultados de su tesis doctoral durante sus estudios en la Escuela Normal Superior de París representan la culminación de un problema de cristalografía que había sido abordado por científicos de renombre, como John Herschel, quien en 1822 demostró la capacidad de los cuarzos para desviar la luz linealmente polarizada; Agustín Fresnel, quien en 1824 demostró que el efecto de la rotación que sufre la luz linealmente polarizada depende de la red interna del cristal ópticamente activo, o Joseph Gay-Lussac y Jean-Baptiste Biot, quienes abordaron sin resolver, en 1826 el primero y en 1832 el segundo, el problema de la inactividad óptica de la llamada sal de paratartrato (Pinilla, 1980). Pasteur trabajó con cristales de 13 tipos de sales obtenidas a partir del ácido tartárico, incluyendo la sal de paratartrato, obtenida del ácido racémico (o paratartárico), y fue el paratartrato la sustancia que le dio la clave para concluir que la actividad óptica de los cristales radica en sus componentes moleculares (no sólo en la red cristalina). Demostró que en realidad el paratartrato es una mezcla de 50% de cristales izquierdos y 50% de cristales derechos de la sal de bitartrato de potasio. De este modo, el llamado ácido racémico era en realidad una mezcla equimolar de moléculas izquierdas y moléculas derechas, las cuales se asocian para formar sus respectivos cristales izquierdos y derechos. Lo anterior explica la aparente inactividad óptica del llamado paratartrato, pues mientras que la mitad de los cristales desvía hacia la izquierda el plano de la luz linealmente polarizada, la otra mitad lo desvía hacia la derecha, contrarrestándose ambos efectos. Con este descubrimiento, Pasteur evidenció la existencia de moléculas izquierdas y derechas, a lo que él llamó disimetría y que es el antecedente de lo que hoy conocemos como quiralidad molecular. Desde muy temprano, Pasteur asoció su descubrimiento con la actividad de los seres vivos: El universo es un conjunto de disimetrías, y estoy convencido de que la vida, tal como se nos manifiesta, es una función de esta disimetría (…) La vida está dominada por acciones disimétricas (de las cuales presentamos la existencia envolvente y cósmica). Incluso presiento también que todas las especies vivientes, en su estructura y en sus formas exteriores son, en un comienzo, funciones de la disimetría cósmica (citado por Pinilla, 1980; Cronnin y Reise, 2005). Esta conjetura hecha por Pasteur en 1870 resulta visionaria, pues la evidencia actual demuestra que todos los seres vivos presentan la propiedad de la homoquiralidad, que consiste en el uso de aminoácidos izquierdos para sintetizar proteínas y del uso exclusivo de desoxirribosa y ribosa derechas para estructurar los ácidos nucleicos (adn y arn). La homoquiralidad es una propiedad que caracteriza a los sistemas vivos, a tal grado que es considerada una condición necesaria para la existencia de la vida. Las teorías actuales acerca del origen de la vida consideran el origen de la homoquiralidad biológica como un paso fundamental. No obstante, diversas preguntas se hallan bajo debate, como el problema de si la homoquiralidad es consecuencia exclusiva del origen y evolución de la vida o si la asimetría quiral forma parte de las condiciones que antecedieron y condujeron al origen de los primeros sistemas biológicos. En el presente trabajo nos inclinamos por esta segunda hipótesis, de tal modo que la asimetría quiral no sólo representa un ingrediente prebiótico más, sino que, como lo argumentaremos, estuvo asociada desde el inicio al flujo de información en los sistemas que potencialmente dieron paso a la vida en la Tierra. En la teoría matemática de grupos, existe un criterio para saber si un objeto o conjunto de puntos es o no quiral. Antes, recordemos que un grupo es una estructura algebraica que se define por la pareja (G, ⊛), donde G es un conjunto no vacío y ⊛ es una operación binaria definida sobre el conjunto G. Para que ⊛ estructure a G como un grupo, dicha operación debe de cumplir:
Un ejemplo es el conjunto de los número enteros ℤ estructurado con la suma, que da como resultado el grupo (ℤ, +), pues al sumar cualesquiera dos números enteros, el resultado es un número entero (la suma es cerrada en ℤ). Además, se cumplen las tres restantes propiedades, conocidas como axiomas de grupo: la suma es asociativa; el número 0 es el elemento neutro para la suma, y para cada número entero, se tiene su inverso aditivo. Un caso particular son los llamados grupos de simetría, que consisten en el grupo (G, ⊛), donde la operación ⊛ es una función llamada simetría, pues da paso a figuras que resultan congruentes con una originalmente dada (es decir, genera figuras que pueden hacerse coincidir entre sí). El ejemplo típico es un cuadrado, donde se pueden rotar sus vértices o se pueden reflejar y siempre se obtiene un “nuevo” cuadrado que puede superponerse sobre el primero. Así, el criterio enuncia que: Un objeto es aquiral si, y sólo si, éste posee un eje impropio de rotación de orden n (citado en Cronin y Reisse, 2005). Donde el orden del eje impropio de rotación es el número de figuras congruentes con la inicial. En otras palabras, dicho orden es el número de arreglos “alternativos” que pueden hacerse coincidir con el objeto dado, después de hacerlo rotar alrededor de un eje situado fuera de la figura (eje impropio). De no cumplirse este criterio, el objeto no puede hacerse coincidir con su imagen obtenida por su reflexión en un plano, por lo que cumple con ser un objeto quiral. Existen concepciones de quiralidad que no se restringen a la propiedad geométrica, sino que incorporan el componente dinámico. Al hacerlo, el comportamiento en el tiempo permite distinguir entre sistemas derechos y sistemas izquierdos. Las nociones de falsa y verdadera quiralidad fueron propuestas en este sentido. La verdadera quiralidad es aquella que resulta de la dinámica del sistema al dar paso a un par especular tanto en términos geométricos como temporales (Buhse et al., 2021). Por su parte, la falsa quiralidad es aquella que se cumple para un sistema en términos geométricos o en términos de su comportamiento en el tiempo, pero no ambos de manera simultánea (figura 2) (Buhse et al., 2021): La verdadera quiralidad está presente en sistemas capaces de existir en dos diferentes estados enantioméricos que pueden interconvertirse por medio de una inversión en el espacio, pero no por una reversión temporal combinada con alguna rotación propia en el espacio (Barron, 2013). Mientras que la falsa quiralidad es exhibida por sistemas que existen en dos diferentes estados enantioméricos que son interconvertidos por medio de una reversión en el tiempo o por medio de una inversión en el espacio (Barron, 2013). En el contexto de la simetría molecular, a los pares especulares o isómeros ópticos se les denomina enantiómeros, de los vocablos griegos ένάντιος (enántios, “opuesto”) y μέρος (méros, “parte”). En 1815, Jean-Baptiste Biot mostró que la luz linealmente polarizada rota su plano de polarización, a favor (derecha) o en contra (izquierda) de las manecillas del reloj al atravesar una sustancia orgánica (Clark, 2019). Esta actividad óptica es la que permite la nomenclatura L/D, para denotar las sustancias levorrotatorias (que desvían el plano de polarización de la luz a la izquierda) y dextrorrotatorias (las que lo hacen hacia la derecha). La nomenclatura actual en la química orgánica se basa en criterios intrínsecos a la geometría molecular, dando paso al sistema R/S, definido por las reglas de Cahn-Ingold-Prelog, que consisten en asignar prioridades de acuerdo a los números atómicos de los grupos de átomos unidos a un centro de simetría (centro estereogénico o estereocentro). Si los grupos de átomos ordenados de mayor a menor según los pesos atómicos siguen una secuencia en el mismo sentido al de las manecillas del reloj, la molécula es definida con una configuración “R” (del latín rectus: derecho). Por el contrario, si la secuencia que se define se da en un sentido contrario al de las manecillas del reloj, el isómero presenta una configuración “S” (del latín sinister: izquierdo). Cuando una reacción química da paso a productos quirales sin que haya alguna influencia asimétrica (como luz circularmente polarizada, vórtices de agitación, sustratos o catalizadores quirales, etcétera), ésta produce mezclas racémicas (una proporción 1:1, equimolar, para ambos enantiómeros). La condición racémica es estable, simétrica y representa el estado de equilibrio termodinámico al que tienden las reacciones. Si alguna fuerza asimétrica influye sobre el sistema y provoca que la reacción se desvíe generando el exceso en uno de los enantiómeros, el producto se vuelve inestable y, en ausencia de la influencia de asimetría, dicho exceso se pierde y alcanza la condición racémica (el equilibrio). Lo anterior es relevante para comprender el papel de la quiralidad en los sistemas vivos, pues en los organismos las reacciones químicas que dan paso a productos asimétricos se mantienen alejadas de la condición racémica. Así, hablar de sistemas vivos es hablar de homoquiralidad, como se afirma en la siguiente definición: Vida es aquello que autorreproduce un ambiente homoquiral (Carroll, 2009). Diversos procesos biológicos son optimizados mediante la homoquiralidad. El espacio al interior de las células es aprovechado mejor si sólo se usan L-aminoácidos, D-desoxirribosa y D-ribosa en lugar del doble de la cantidad de estas moléculas si estuvieran en proporciones racémicas. También la velocidad en las reacciones químicas catalizadas por enzimas se hace eficiente, pues al ser polímeros compuestos por L-aminoácidos, las enzimas presentan una complementariedad geométrica con moléculas quirales, por lo que se facilita el reconocimiento de sustratos por parte del sitio catalítico. Otro proceso optimizado por la homoquiralidad es el de asociar ciertas dinámicas celulares con un enantiómero particular, como en los receptores moleculares, pues al reconocer uno u otro isómero óptico, las células son capaces de relacionarse con el entorno. Por ejemplo, el reconocimiento del R-limoneno (presente en la cáscara de las naranjas) y del S-limoneno (en la cáscara de los limones) permite diferenciar e identificar ambos frutos mediante su aroma por parte de los receptores sensoriales olfativos. Los isómeros ópticos, al diferir únicamente en la orientación espacial de sus grupos de átomos a manera de imagen especular, tienen las mismas propiedades físicas y químicas. Sin embargo, en un ambiente con asimetría, los enantiómeros se diferencian entre sí debido a que establecen interacciones distintas con el medio. Éste es el caso en los sistemas vivos. La asimetría quiral en las células no sólo se restringe a los L-aminoácidos, D-desoxirribosa y D-ribosa, sino que hay una variedad de moléculas que se encuentran en proporciones asimétricas, como la D-glucosa o la D-fructosa. El fármaco derivado del aminoácido L-glutamina, llamado talidomida, es un ejemplo de cómo los enantiómeros interactúan de manera distinta en un ambiente con asimetría quiral. La talidomida fue sintetizada en 1952 en Alemania como parte de un programa de investigación para desarrollar nuevos antibióticos. En 1956 fue comercializada en Europa como un sedante para tratar el insomnio, dolores de cabeza y resfriados. La talidomida es una molécula que se encuentra en proporciones racémicas, donde la R-talidomida es la forma que presenta los efectos sedantes. Por su parte, la S-talidomida no tiene efectos en los adultos, pero sí sobre embriones en desarrollo: afecta la formación de extremidades (brazos y piernas), provocando malformaciones anatómicas en órganos como el corazón o afecciones en el desarrollo de los nervios periféricos. A partir de 1961 fue regulada su administración durante el embarazo, debido al nacimiento de niños con graves defectos teratogénicos. Además de la asimetría quiral en moléculas individuales, los excesos enantioméricos determinan la asimetría en ensambles macromoleculares. Las proteínas, formadas por L-aminoácidos, presentan motivos estructurales en forma de α-hélices que se tuercen hacia la derecha en torno a un eje de simetría externo, motivo por el cual a este tipo de quiralidad se le denomina axial. En condiciones fisiológicas estándar, el adn estructurado por D-desoxirribosa también presenta quiralidad axial, donde el giro de su estructura helicoidal se da hacia la derecha, al igual que lo hace el arn cuando forma estructuras de doble cadena. En un nivel de organización mayor, la proteína estructural llamada colágeno, presente en los mamíferos como el principal componente de la matriz extracelular que da soporte al tejido conectivo, el cartílago o la piel, se forma por la asociación de tres hélices sinistrales, que unidas dan paso a una superhélice (estructura cuaternaria) que gira hacia la derecha. Subiendo en el nivel de organización, la asociación de macromoléculas para formar organelos celulares también da paso a estructuras quirales. Los cilios, presentes en organismos unicelulares que constituyen el grupo taxonómico de los ciliados, tienen un arreglo proteico en la base (cuerpo basal) que exhibe un ordenamiento dextral (Inaki et al., 2016). Este ejemplo es interesante debido a que estas estructuras forman parte de todo el organismo (que es unicelular), de modo tal que cuando los cilios se ensamblan formando la infraciliatura, la corteza celular resulta ser una estructura quiral a nivel de la célula completa, donde los cilios adoptan conjuntamente un movimiento a favor del sentido de las manecillas del reloj. A este nivel anatómico, la quiralidad está presente desde el desarrollo embrionario de los animales: el eje lateral, definido después de las primeras rupturas de la simetría en un cigoto mediante los ejes antero-posterior y dorso-ventral, da paso a una anatomía quiral. Entre los estadios embrionarios 12 y 13 de la mosca de la fruta, Drosophila, el intestino grueso en desarrollo rota 90° en sentido antihorario, se posiciona de manera asimétrica en el eje lateral y genera una asa que abre hacia el lado derecho (figura 3a), siendo el primer órgano que hace visible la asimetría en el embrión de la mosca (Inaki et al., 2016). En cuanto a la anatomía exterior, los caracoles gasterópodos presentan una concha dorsal en espiral que puede ser dextrógira, como en la especie Lymnaea stagnalis; o levógira, como en la especie Physa acuta (figura 3b) (Inaki et al., 2016). En los vertebrados, el posicionamiento asimétrico de los órganos viscerales y abdominales también define una anatomía quiral. El corazón en los mamíferos se encuentra posicionado ligeramente a la izquierda, así como el estómago. El pulmón izquierdo es más pequeño que el derecho, y el colon y el apéndice se encuentran posicionados hacia la derecha (figura 3c). En el caso de las plantas, estructuras como los zarcillos presentan quiralidad. Existen especializaciones en los tallos de algunos tipos de plantas trepadoras que se enroscan alrededor de un eje, lo que les permite acceder a la luz solar. Los zarcillos presentan un crecimiento helicoidal, ya sea dextral o sinistral, dependiendo de la especie de planta (figura 3d). La quiralidad en los componentes a distintos niveles de organización biológica permite asociar la asimetría con ciertas funciones. La anatomía helicoidal ayuda a optimizar el espacio corporal al enrollar la longitud del organismo entorno al eje de simetría (como en los caracoles). El enrollamiento interno en el caso del intestino de los vertebrados aumenta la longitud de este órgano mientras queda contenido en el animal, haciendo eficiente la extracción de la energía durante la digestión; por ejemplo, en los rumiantes, la longitud del intestino llega a ser de poco más de veinte veces la longitud del animal (Blum et al., 2014). Por lo tanto, la asimetría quiral en los sistemas vivos no sólo es una característica, sino una propiedad funcional. En particular, a nivel molecular enfatizamos que la asimetría quiral permite reducir la incertidumbre en las células, pues dentro de los sistemas vivos no hay ambigüedad en el uso de moléculas izquierdas o derechas, según sea el caso. Podemos afirmar que los seres vivos son capaces de mantener sus procesos biológicos debido a que son sistemas homoquirales. La teoría de la autopoiesis hace referencia a un tipo de organización en sistemas que son capaces de producirse a sí mismos (Varela et al., 1974). Afirma que los procesos biológicos están soportados en última instancia por la organización y dinámica molecular. Propiedades a gran escala como la evolución o la adaptación, así como aquéllas a corto plazo, como la reproducción, sólo son posibles gracias a esa organización a manera de red autopoiética. Esta organización incluye además procesos para sintetizar sus componentes y mecanismos que posibilitan retirar los elementos dañados para colocar en su lugar aquéllos recién sintetizados. Lo anterior les permite a los seres vivos propagarse y perdurar más tiempo del que lo hacen sus componentes por separado. La red autopoiética molecular que define a los sistemas vivos debe ser también capaz de automantener un ambiente homoquiral. Al presentar la misma quiralidad, se reduce la incertidumbre en las interacciones entre los componentes moleculares. Esto permite un vínculo con la teoría de la información (Shannon, 1948), pues se dice que un elemento contiene información si reduce la incertidumbre en el sistema. En los seres vivos, la información puede entenderse como una dinámica compleja que vincula la organización (molecular) con las funciones biológicas (Cruz-Rosas et al., 2020). La expresión genética es evidencia de este vínculo entre la organización y las funciones, pues los componentes moleculares que censan las variables en el medio (externo o interno) inducen la síntesis de componentes (proteínas), que se incorporarán a una función específica como respuesta a las condiciones censadas. Este tipo de información es secuencial, pues se encuentra codificada en la disposición en que aparecen los monómeros en un polímero (bases nitrogenadas en el adn o en el arn. El modelo llamado Dogma Central de la Biología Molecular (Crick, 1970) explica que el flujo de este tipo de información se puede dar entre los ácidos nucleicos (adn y arn) y de éstos hacia las proteínas, pero establece que el flujo de información secuencial nunca puede darse de proteínas hacia ácidos nucleicos. Es decir, una secuencia de aminoácidos no puede determinar una secuencia de adn o de arn. Además, el flujo de secuencias entre las proteínas tampoco es posible. A pesar de la validez de este modelo, cada vez hay más observaciones que ponen de manifiesto que es insuficiente para describir la dinámica de la información biológica. Los seres vivos también hacen uso de las geometrías moleculares para organizarse y para regular sus funciones de acuerdo con el contexto ambiental. A nivel molecular, las enzimas reconocen sus sustratos por medio de la forma y el complemento geométrico en el sitio activo (figura 4a). Las células hacen uso de proteínas en sus membranas para detectar la presencia de moléculas que les permite la comunicación célula-célula, como en la sinapsis química, la comunicación entre poblaciones de células por medio de hormonas o el reconocimiento de células contiguas que expresan otras proteínas en sus membranas o en la matriz extracelular (figura 4b). Tales mecanismos de reconocimiento molecular dependen de la forma de los componentes implicados, donde la complementariedad geométrica y el acoplamiento espacial son fundamentales. A nivel de organismos pluricelulares, en los vertebrados, la respuesta adaptativa del sistema inmune hace uso de la geometría molecular: cuando algún agente infeccioso es degradado por los macrófagos, éstos exponen los segmentos del patógeno por medio del complejo mayor de histocompatibilidad, para que las células T tomen un molde de la geometría molecular, el cual transfieren a las células B para que lo expresen en las proteínas inmunoglobulinas (los anticuerpos), que van a circular por el torrente sanguíneo portando esa información para reconocer al patógeno mediante las referencias en la forma molecular de sus componentes (Cruz-Rosas et al., 2020) (figura 4c). Sobre la base de lo expuesto, podemos reconocer dos tipos de polímeros informacionales en los sistemas vivos: los ácidos nucleicos, capaces de codificar la información secuencial, y las proteínas, capaces de contener la información geométrica (Cruz-Rosas et al., 2020). En ambas moléculas, la homoquiralidad optimiza el flujo de información, pues el uso de D-desoxirribosa y D-ribosa en el adn y arn permite orientar las bases nitrogenadas en la misma dirección, haciendo que los procesos de copiado y decodificación tengan la información precisa del tipo de nucleótido presente en cada posición. En el caso de las proteínas, el uso de L-aminoácidos también determina la misma orientación espacial de sus cadenas laterales, reduciendo las interferencias electrostáticas o hidrofóbicas durante los acoplamientos y reconocimientos supramoleculares. Por lo tanto, la homoquiralidad molecular es una propiedad funcional que optimiza el flujo de información en los sistemas vivos. Barron, L. D. (2013). True and false chirality and absolute enantioselection. Rend. Fis. Acc. Lincei, 24(3), 179-189. https://link.springer.com/content/pdf/10.1007/s12210-013-0224-6.pdf Blum, M., Feistel, K., Thumberger, T. y Schweickert, A. (2014). The evolution and conservation of left-right patterning mechanisms. Development, 141(8), 1603-1613. https://doi.org/10.1242/dev.100560 Buhse, T., Cruz, J. M., Noble-Teran, M. E., Hochberg, D., Ribó, J. M., Crusats, J. y Micheau, J. C. (2021). Spontaneous deracemizations. Chemical Reviews, 121(4), 2147-2229. https://doi.org/10.1021/acs.chemrev.0c00819 Carroll, J. D. (2009). A new definition of life. Chirality, 21(3), 354-358. https://doi.org/10.1002/chir.20590 Clark, E. (2019). Pioneers in Optics: Jean-Baptiste Biot. Microscopy Today, 27(2), 40-41. https://doi.org/10.1017/S1551929519000014 Crick, F. (1970). Central dogma of molecular biology. Nature, 227(5258), 561-563. https://doi.org/10.1038/227561a0 Cronin, J. y Reisse, J. (2005). Chirality and the origin of homochirality. Second edition. En Lectures in astrobiology (pp. 473-515). Springer. https://link.springer.com/content/pdf/10.1007%2F10913406_14.pdf Cruz-Rosas, H. I., Riquelme, F., Ramírez-Padrón, A., Buhse, T., Cocho, G. y Miramontes, P. (2020). Molecular shape as a key source of prebiotic information. J Theor Biol, 499, 110316. https://doi.org/10.1016/j.jtbi.2020.110316 Inaki, M., Liu, J. y Matsuno, K. (2016). Cell chirality: its origin and roles in left-right asymmetric development. Phil Trans R Soc B, 371(20150403). http://dx.doi.org/10.1098/rstb.2015.0403
Pinilla, R. 1980. Pasteur. En Genios y lideres de la historia, Vol. xi (pp. 11-125). Promexa.
Shannon, C. E. (1948). A mathematical theory of communication. Bell Labs Tech J, 27(3), 379-423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x Varela, F. G., Maturana, H. R. y Uribe, R. (1974). Autopoiesis: The organization of living systems, its characterization and a model. Biosystems, 5(4), 187-196. https://doi.org/10.1016/0303-2647(74)90031-8
orcid: 0000-0003-2451-544X/quetzal.hi@gmail.com
Investigador Posdoctoral Conacyt/Centro de Investigacions Químicas (ciq), Universidad Autónoma del Estado de Morelos (uaem)
orcid: 0000-0002-6435-5551/ntme_fc@uaem.mx
Centro de Investigacions Químicas (ciq), Universidad Autónoma del Estado de Morelos (uaem)
orcid: 0000-0003-3306-5137/jmcm@unach.mx
Facultad de Ciencias en Física y Matemáticas (fcfm), Universidad Autónoma de Chiapas (unach)
orcid: 0000-0001-5082-0873/buhse@uaem.mx
Centro de Investigacions Químicas (ciq), Universidad Autónoma del Estado de Morelos (uaem)
resumen
abstract
palabras clave
key words
Introducción
Figura 1
Ejemplo de objeto quiral y su no superponibilidad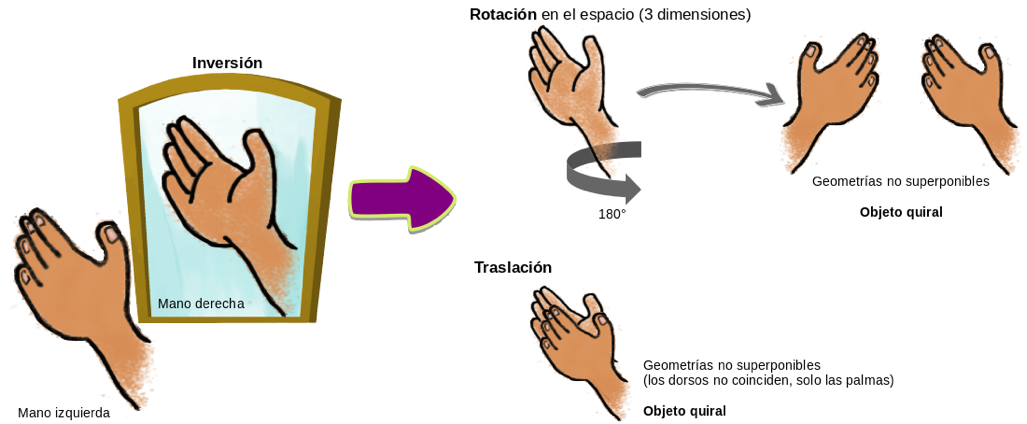
Fuente: Elaboración propia
La quiralidad es una propiedad geométrica
Figura 2
Verdadera y falsa quiralidad inducidas por el movimiento
Fuente: Elaboración propia.
Moléculas quirales
Quiralidad en la biología
Figura 3
Anatomía quiral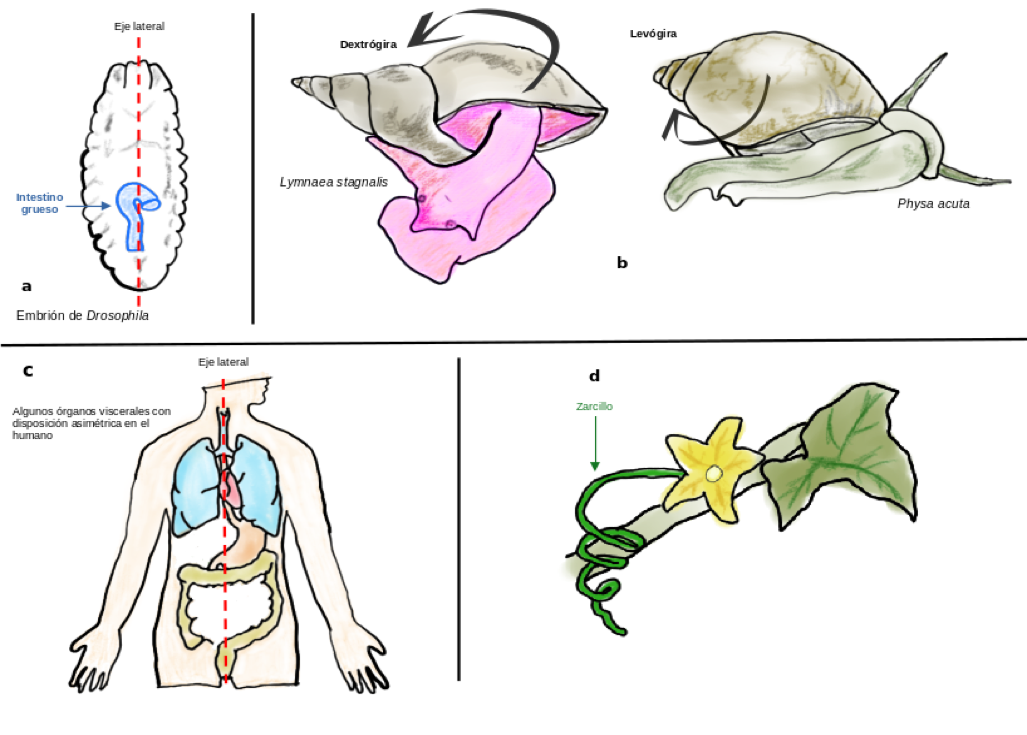
Fuente: Elaboración propia.
Quiralidad e información en los sistemas vivos
Figura 4
Reconocimiento molecular basado en la geometría (información conformacional)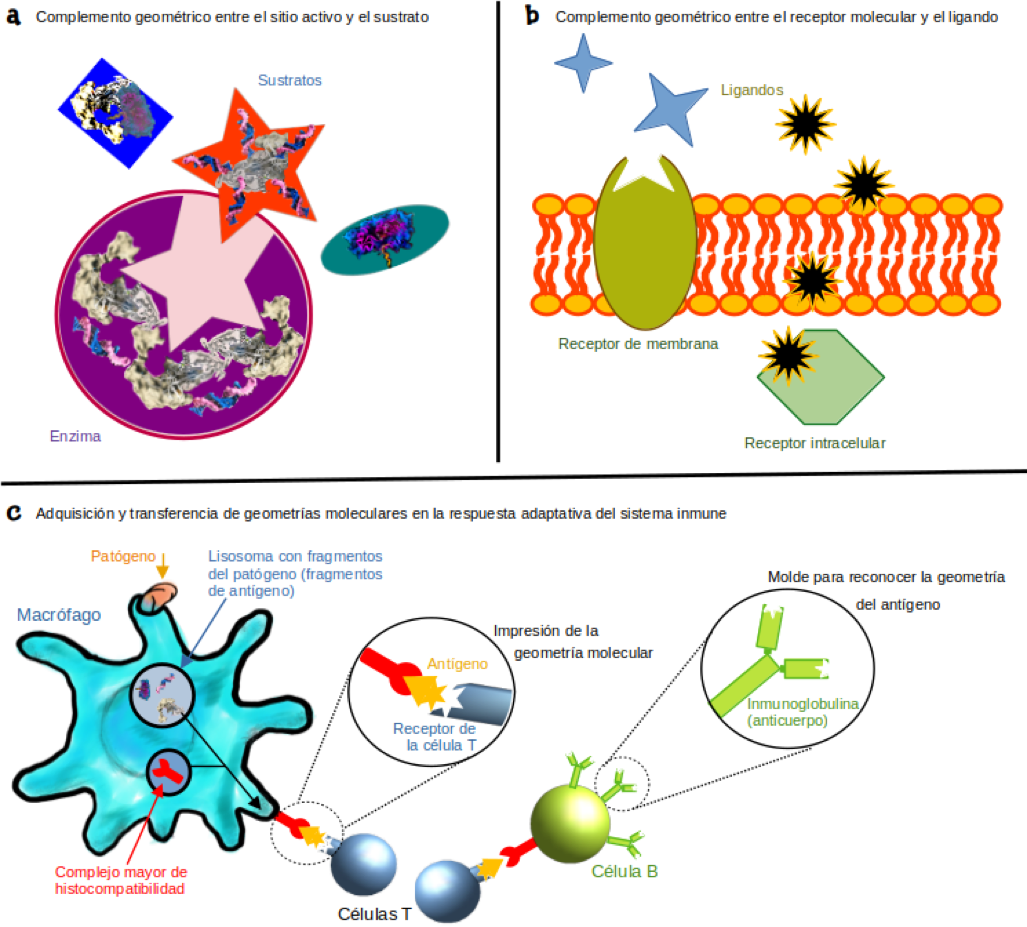
Fuente: Elaboración propia.
Referencias