Año 17, núm. 42, julio 2021
doi: http://doi.org/10.30973/inventio/2021.17.42/5
Tratamiento de los problemas verbales en los libros de texto de matemáticas
Treatment of word problems in mathematics textbooks
Julio Tarín Ibáñez Raúl Tárraga Mínguez Los libros de texto son el tipo de material curricular más empleado en la educación obligatoria. El objetivo de este trabajo es analizar el tratamiento que reciben los problemas aritméticos verbales de estructura aditiva en estos materiales. Se llevó a cabo una revisión de estudios recientes que analizan la estructura semántica de los problemas en los libros de texto de diferentes sistemas educativos. Se concluye que los libros de texto no constituyen, por sí solos, herramientas eficaces para abordar el proceso de enseñanza-aprendizaje de la resolución de problemas. Además, es necesario tener en cuenta las carencias de estos materiales curriculares y utilizar problemas matemáticos que abarquen todas las estructuras semánticas. Textbooks are the most widely used type of curricular material in compulsory education. The objective of this work is to analyze the treatment received by verbal arithmetic problems with additive structure in these materials. We carried out a review of recent studies that analyze the semantic structure of problems in textbooks from different educational systems. The conclusion is that textbooks are not, by themselves, effective tools to address the teaching-learning process of problem solving. In addition, it is necessary to take into account the shortcomings of these curricular materials and use mathematical problems that cover all semantic structures.
análisis curricular, libros de texto, problemas verbales de
estructura aditiva curricular analysis, textbooks, verbal problems with additive
structure Se puede afirmar con rotundidad que, tanto en el ámbito nacional como en el internacional, el libro de texto ocupa una posición hegemónica en el proceso de enseñanza-aprendizaje de las matemáticas, de manera que constituye el principal recurso material utilizado por los docentes en la práctica diaria del aula (Apple, 1992; Boesen et al., 2014; Hansen, 2018; Van Stiphout, 2011). De hecho, los libros de texto de matemáticas determinan en gran medida qué enseñan los profesores y, en consecuencia, qué aprenden los alumnos, puesto que, en muchas ocasiones, su papel es incluso más decisivo que las propias prescripciones del currículo oficial (Cai y Jiang, 2017; Kolovou et al., 2009; Monterrubio y Ortega, 2012). Así, si un contenido matemático no aparece incluido en el libro de texto, probablemente no será estudiado en el aula (Wijaya et al., 2015). A pesar de que el libro de texto puede ser utilizado con cierta flexibilidad, la investigación apunta a que, en general, el comportamiento de los docentes es muy consistente con los contenidos, el orden de presentación de éstos en las unidades didácticas y el enfoque metodológico que este material adopta (Despina y Harikleia, 2014; Vincent y Stacey, 2008). De este modo, las editoriales se convierten en el agente más decisivo a la hora de determinar el currículo real, que es establecido en función de las creencias de un determinado autor o grupo de autores sobre los contenidos matemáticos que deben ser considerados relevantes, sobre los procesos de enseñanza-aprendizaje, sobre lo que es un problema y sobre el papel que debe desempeñar la resolución de problemas (rp) en el aula (López et al., 2015). Wijaya et al. (2015) señalan que, como consecuencia de esta influencia y sus efectos en la práctica educativa, muchos estudios se han dirigido a investigar el tratamiento de diferentes contenidos matemáticos en los libros de texto, entre ellos, los problemas y su proceso de resolución, dada su importancia en los currículos de los sistemas educativos de los países avanzados. Algunos de estos trabajos han sido desarrollados en el contexto de estudios comparativos sobre la rp con los libros de texto utilizados en diferentes países (Cai y Jiang, 2017; Depaepe et al., 2009; Van Zanten y Van den Heuvel-Panhuizen, 2018). En otras investigaciones, como la desarrollada por Ruiz (2013), se ha estudiado la estructura de las unidades didácticas en los textos escolares y el tratamiento que se ha dado a la rp en ellas, esto es, enseñanza para la rp (problemas como práctica rutinaria), sobre la rp (problemas como habilidad) y a través de la rp (problemas como vehículo y arte). Asimismo, no faltan las investigaciones destinadas a estudiar las distintas percepciones que los profesores tienen de los libros de texto de matemáticas, así como la frecuencia de su uso y las modificaciones que los docentes efectúan en ellos (Horsley y Sikorová, 2014). Por último, son abundantes los estudios que han analizado diversas variables de los problemas contenidos en los libros de texto: su carácter rutinario (identificado con el ejercicio mecánico y reproductivo) frente a su carácter no rutinario (Marchis, 2012; Van Zanten y Van den Heuvel-Panhuizen, 2018); el grado de desafío relativo a la información del problema, como la información superflua o datos de más, o la información ausente o datos de menos (Orrantia et al., 2005; Wijaya et al., 2015); el grado de desafío referente a las tareas de planteamiento o invención de problemas por parte de los alumnos (Cai y Jiang, 2017; Marchis, 2012; Orrantia et al., 2005); el contexto situacional donde aparecen los problemas (Brehmer et al., 2016; Orrantia et al., 2005; Ozer y Sezer, 2014; Wijaya et al., 2015); y finalmente, la estructura semántica de los problemas aritméticos verbales (pav) de estructura aditiva. Precisamente, la finalidad de este artículo es llevar a cabo una revisión del tratamiento que dan los libros de texto de matemáticas a los pav, esto es, a los problemas que habitualmente resuelven los escolares en la etapa primaria, tomando como referencia algunas de las investigaciones más relevantes (nacionales e internacionales) realizadas en la última década. Nos centramos en el análisis de la estructura semántica de los problemas, uno de los factores más relevantes en el análisis de los pav. Tras la síntesis de la revisión de estudios que han analizado esta variable, exponemos las conclusiones que se derivan de estas investigaciones y lanzamos algunas propuestas de cara a una mejora educativa. Desde los años veinte del siglo pasado, el conductismo fue el modelo dominante en la educación en general y, por consiguiente, en la educación matemática. La perspectiva behaviorista centra su interés en la conducta directamente observable, que será estudiada en términos de estímulos y respuestas externas, sin tener en cuenta los procesos internos que subyacen al proceso de enseñanza-aprendizaje. En consecuencia, el estudio de las variables cognitivas y afectivas será desplazado a un lugar secundario, al ser consideradas procesos internos y subjetivos, y por ello difíciles de observar y cuantificar. Desde esta perspectiva, los contenidos matemáticos constituyen un conglomerado de datos y reglas, técnicas o procedimientos que el alumno, como mero receptor pasivo, deberá imprimir en su mente a través de la ejecución reiterativa de ejercicios de carácter mecánico y rutinario. Con la “primera oleada de la revolución cognitiva” (De Corte et al., 1996), durante los años ochenta, comienza a surgir un interés creciente por la comprensión de los procesos mentales que se ponen en marcha durante la ejecución de tareas matemáticas complejas, como
la rp, con lo que se produce “un giro hacia lo cognitivo” (Sarabia e Iriarte, 2011, p. 26). En ese momento, diversos trabajos comienzan a analizar cómo los niños resuelven problemas simples de estructura aditiva, pero un elemento clave que emerge en estos primeros trabajos, y que posteriormente ha guiado buena parte de la investigación, es la distinción de tres clases de situaciones problemáticas, denominadas cambio, combinación y comparación (Heller y Greeno, 1978), y posteriormente una nueva categoría denominada igualación (Carpenter y Moser, 1983), que combina las categorías de cambio y comparación. Así, para clasificar los pav deja de ponerse el acento en variables superficiales (el número de palabras existentes en el problema, el orden de las proposiciones en el enunciado, el tipo de vocabulario o la complejidad sintáctica del texto problema), y la investigación se centra en la estructura semántica, esto es, una representación del texto verbal en términos de relaciones semánticas entre las cantidades del enunciado dependiendo de la categoría del problema (cambio, combinación, comparación o igualación), es decir, en términos de esquemas semánticos. Por ejemplo, el problema de cambio 1: Juan tenía 8 canicas; en una partida ganó 3. ¿Cuántas canicas tiene ahora Juan? supondría, tal como se muestra en la figura 1, activar el esquema de cambio y asignar las cantidades del enunciado a cada una de las categorías del esquema semántico (conjunto inicial, canicas que tiene ahora Juan = 8; conjunto de cambio, lo que se añade = 3; y conjunto final, resultado = 11). Cada una de estas categorías se divide, a su vez, en seis subcategorías en los problemas
de cambio, comparación e igualación, y en dos categorías en los problemas de combinación. De este modo, contamos con un total de veinte pav de estructura aditiva simples, que pueden combinarse entre sí y dar lugar a los pav de estructura aditiva compuestos. En general, existe un consenso en señalar que los problemas de cambio son los más sencillos de resolver (p. ej. problema de cambio 2: Juan tiene 8 canicas; en una partida pierde 5 canicas. ¿Cuántas canicas le quedan ahora?), seguidos muy de cerca de los problemas de combinación (p. ej. problema de combinación 1: Juan tiene 5 canicas. Pedro tiene 3 canicas. ¿Cuántas canicas tienen entre los dos?). Posteriormente, se situarían los problemas de igualación (p. ej. problema de igualación 1: Juan tiene 5 canicas. Pedro tiene 8 canicas. ¿Cuántas canicas tiene que ganar Juan para tener las mismas que Pedro?). Y, por último, los de comparación (p. ej. problema de comparación 1: Juan tiene 5 canicas. Pedro tiene 8 canicas. ¿Cuántas canicas tiene Pedro más que Juan?). Ahora bien, este orden de dificultad en función de la categoría semántica debe matizarse, ya que la posición de la incógnita o cantidad desconocida determina igualmente la dificultad del problema. En efecto, los alumnos presentan menores dificultades cuando la incógnita se sitúa en el resultado (a + b = ?). La dificultad aumenta cuando la incógnita se sitúa en el segundo sumando (a + ? = c); y la máxima dificultad aparece cuando el término desconocido es el primero (? + b = c). Veamos estos tres ejemplos de problemas de cambio: Juan tiene 3 canicas; en una partida gana 5 canicas. ¿Cuántas canicas tiene ahora? (incógnita en el resultado, 3 + 5 = x); Juan tiene 3 canicas; en una partida gana algunas canicas. Ahora Juan tiene 8 canicas. ¿Cuántas canicas ha ganado? (incógnita en el segundo sumando, 3 + x = 8); Juan tiene algunas canicas; en una partida gana 5 canicas. Ahora Juan tiene 8 canicas. ¿Cuántas canicas tenía? (incógnita en el primer sumando, x + 5 = 8). Además de la posición de la incógnita, otra variable que condiciona la dificultad de los
pav es su consistencia o inconsistencia. En efecto, Lewis y Mayer (1987) propusieron una clasificación alternativa de tipo dicotómico, fundamentada en la coherencia o consistencia entre la estructura superficial del problema y el algoritmo necesario para resolverlo; de este modo distinguieron entre problemas consistentes e inconsistentes. Así, los problemas canónicos o expresados con un lenguaje consistente resultan más sencillos de resolver que los no canónicos o inconsistentes. La mayor facilidad de los primeros radica en la existencia de una coherencia entre la estructura superficial del problema y la operación aritmética con que se resuelve; p. ej. en el problema “Cemre tiene 56 galletas y Selim tiene 34. ¿Cuántas galletas tiene Selim menos que Cemre?” (Tarim, 2017, p. 664), la palabra clave menos indica que el algoritmo que debe ejecutarse es la resta. Sin embargo, en los problemas inconsistentes esta palabra clave indica la operación contraria, p. ej. en el problema propuesto por la misma autora: “Ayla tiene 29 caramelos y su hermana Elif tiene 44. ¿Cuántos caramelos tiene Elif más que Ayla?”, la palabra más indica la operación contraria. De acuerdo con la hipótesis de la consistencia, son consistentes los problemas de combinación 1; de cambio 1, 2 y 4, y de comparación e igualación 2, 3 y 4. Por otra parte, son inconsistentes los problemas de combinación 2; de cambio 3, 5 y 6, y de comparación e igualación 1, 5 y 6. Para alcanzar nuestro objetivo de revisar el tratamiento que dan los libros de texto de matemáticas a los pav, se realizó una búsqueda en la base de datos Scopus, introduciendo en los campos de título, resumen y palabras clave los términos de búsqueda “mathematics”, “textbooks” y “problem solving”, y restringiendo la búsqueda a los artículos publicados entre el año 2000 y octubre de 2021. Como resultado, la base de datos devolvió un total de 247 documentos. Los autores del
estudio procedimos a la lectura del título y resumen de estos artículos para seleccionar únicamente aquellos que habían analizado de manera sistemática la estructura semántica de todos los pav de un conjunto amplio de libros de texto de al menos una editorial. No se incluyeron estudios que analizaran problemas aislados de un conjunto indeterminado de libros de texto, sino únicamente los que analizaran de manera sistemática el conjunto de libros de texto de una editorial para todos los cursos de educación primaria; o el conjunto de los libros de texto de varias editoriales para un curso concreto de educación primaria. Tras aplicar estos criterios de exclusión, se seleccionaron finalmente seis estudios (tabla 1), de los que se elaboró un análisis de contenido para determinar qué tipo de análisis realizaron y sus resultados. El análisis de contenido se hizo teniendo en cuenta que el interés del presente artículo es determinar qué tipología de problemas se incluye en los libros de texto de acuerdo con su estructura semántica y si esta tipología corresponde o no a una metodología de enseñanza en la que los problemas matemáticos son una herramienta pedagógicamente útil para el aprendizaje de los estudiantes. La síntesis de las principales características de los estudios incluidos en la presente revisión se expone en la tabla 1. Tras la tabla se exponen de manera narrativa los principales resultados y conclusiones alcanzados en cada estudio. Con el objeto de presentar un panorama general del papel que desempeñan los problemas en los libros de texto y las prácticas escolares promovidas por éstos, Orrantia et al. (2005) llevaron a cabo un estudio pionero en España, donde se analizaron los pav de estructura aditiva de tres editoriales. Los resultados evidenciaron que, en general, las tres editoriales mostraban un panorama muy similar, caracterizado por una escasa variedad de subtipos de problemas y una alta frecuencia de problemas consistentes para cuya resolución no era necesario aplicar un conocimiento conceptual avanzado ni sofisticadas estrategias de resolución. Así, la mayoría de estos problemas podían ser resueltos por los alumnos mediante la estrategia de la palabra clave (p. ej. “más” o “ganar” = sumar; “menos” o “perder” = restar), que puede aplicarse de forma mecánica sin necesidad de una comprensión genuina del problema. Por otra parte, los resultados del análisis de los problemas compuestos revelaron la misma tendencia encontrada en los problemas simples. Un segundo estudio desarrollado en España fue el de Chamoso et al. (2014), donde se planteó comprobar hasta qué punto el panorama descrito en el estudio precedente de Orrantia et al. (2005) había cambiado. Los resultados mostraron nuevamente una limitada variabilidad de subcategorías y una alta proporción de problemas consistentes. Según los autores, esta distribución de los problemas, concentrados prácticamente en categorías consistentes, muestra la visión limitada de las situaciones problemáticas de estructura aditiva presentadas por el libro de texto. Esta visión reducida en cuanto a la variabilidad y escasa frecuencia de problemas inconsistentes puede significar, según los autores, que los alumnos terminen por automatizar la estrategia de la palabra clave, estrategia superficial que no les ayudará cuando tengan que enfrentarse a situaciones problemáticas no tan sistemáticas. Así, para estos autores es razonable pensar que cuando un alumno se enfrente por ejemplo a un problema inconsistente de comparación 5 (que no aparece ni una sola vez en los libros de texto) utilice estrategias informales y no estrategias aprendidas en la escuela, puesto que el alumno no puede aplicar aquello que no ha aprendido. Por otro lado, en el estudio de Vicente et al. (2018) se analizaron los pav de estructura aditiva y multiplicativa con el propósito de conocer su grado de complejidad, tanto a nivel procedimental (número de pasos necesarios para resolver el problema) como a nivel semántico-matemático (estructura y subestructura semántica). Con respecto a la complejidad semántico-matemática, objeto de esta revisión, los resultados no variaron sustancialmente con respecto a los dos estudios precedentes. En concreto, el 77.21% de los pav de estructura aditiva y multiplicativa fueron de complejidad baja, el 19.19% media y tan sólo el 3.19% alta. Otro hallazgo interesante fue que en los cursos superiores no se encontraron pav de mayor complejidad que en los cursos inferiores, ni tampoco hubo diferencias notables entre los resultados de las dos editoriales analizadas. Los autores concluyen que la dieta instruccional propuesta por los libros de texto se caracteriza por una escasa variedad de pav aditivos y multiplicativos, que pueden ser resueltos por los alumnos mediante el uso de estrategias superficiales, en detrimento de modos genuinos de resolución donde se hace necesaria la intervención del razonamiento. Finalmente, el estudio más reciente en España es el realizado por Tárraga et al. (2021), en el que se utilizaron las mismas editoriales que en el estudio pionero de Orrantia et al. (2005) y se analizaron las mismas variables: estructura semántica, grado de desafío y contexto situacional donde aparecen los problemas en los libros de texto desde el año 2014 hasta la actualidad. Con respecto a la estructura semántica, del total de problemas analizados (1 900), 1 628 (85.3%) fueron consistentes, frente al 14.6% que resultaron inconsistentes. Asimismo, hubo una escasa variabilidad de categorías y subcategorías, al igual que en los estudios precedentes. El subtipo de combinación 1 fue el más frecuente de toda la muestra, seguido de los subtipos de cambio 1 y 2. El resto de los problemas de cambio apenas aparecieron en el análisis. En cuanto a la categoría de comparación, el subtipo más numeroso fue el de comparación 1 (7.10%) de naturaleza inconsistente. El resto de los subtipos de comparación tuvieron una presencia mínima o nula. Por último, los problemas de igualación fueron los que presentaron los índices más bajos, tanto con respecto a la frecuencia como a la variabilidad, pues de los seis subtipos únicamente fueron incluidos por las editoriales, con porcentajes mínimos, el subtipo igualación 1 (0.68%) e igualación 2 (0.22%). Siguiendo a Lester (2013), los autores concluyen que la investigación educativa ha puesto de relieve, por un lado, que para que se produzca una mejora en la habilidad de rp los alumnos tienen que trabajar en tareas problemáticas de una manera regular durante un periodo prolongado, esto es, aumentar la frecuencia de problemas en los libros de texto; por otro, que los alumnos mejorarán como solucionadores de problemas sólo si se les brindan suficientes oportunidades para resolver una variedad de tipos de tareas problemáticas en las que se aumente la variabilidad de categorías y subcategorías. En el ámbito internacional, dos de los estudios más actuales que se han ocupado de analizar la estructura semántica de los pav en los libros de texto son el estudio de Despina y Harikleia (2014), por un lado, y el estudio de Tarim (2017), por el otro; ambos basados en las investigaciones precedentes llevadas a cabo en Turquía por Olkun y Toluk (2002), y en Malasia por Singh y Teoh (2010). El análisis conjunto de ambos estudios mostró que, al igual que en los estudios precedentes, los pav más numerosos presentados por los libros de texto fueron los más sencillos de resolver; por medio de esto se constató igualmente una escasa variabilidad de subtipos de pav, de manera que la tipología de problemas incluidos en los libros de texto de los diferentes cursos analizados resultó ser básicamente la misma. Además, en el estudio de Despina y Harikleia (2014) se evidenció que la proporción de pav incluidos en los libros de texto resultaba muy escasa (83 problemas en el primer curso y 111 problemas en el segundo), lo que supone que las oportunidades que se ofrecen a los alumnos para aprender a resolver problemas se limitan a la realización de dos o tres problemas por semana. En el estudio de Tarim (2017), el número de pav presentados en los libros de texto, lejos de aumentar, iba disminuyendo de un nivel educativo a otro superior. De este modo, de los 139 problemas analizados por la autora, 91 se encontraban en los libros de texto del primer curso, mientras
que en el segundo curso hubo 36 y en el tercero tan sólo 12. En el estudio de Despina y Harikleia (2014), las autoras concluyen, por un lado, que es muy posible que la comprensión conceptual o matemática de las diferentes situaciones aditivas
se vea inhibida debido a las escasas oportunidades que se ofrecen a los alumnos en los libros
de texto. Sin embargo, también es posible que los alumnos se enfrenten con ciertas dificultades en la rp al no estar expuestos a una variedad suficiente de problemas con estructuras semánticas diferentes. Por su parte, Tarim (2017) concluye que los libros de texto analizados no responden a una planificación sistemática donde se tenga en cuenta una graduación de la dificultad de los problemas, o la presencia equilibrada de las diferentes categorías y subcategorías de pav. Además, la autora refiere que transcurridos quince años desde el último estudio sobre el tratamiento de los problemas en Turquía no se observan mejoras sustanciales. La investigación actual ha puesto de manifiesto que el libro de texto desempeña un papel hegemónico en la mayoría de los sistemas educativos (Escudero, 2015; Fuchs y Bock, 2018; Hansen, 2018). Dado que el proceso de enseñanza-aprendizaje de las matemáticas no está exento de esta influencia, el objetivo de esta revisión se ha dirigido a ofrecer al lector una visión general sobre el tratamiento de los problemas en los libros de texto de matemáticas a través de algunas de las investigaciones más relevantes publicadas en los últimos años. Esta revisión nos ha permitido caracterizar las situaciones problemáticas presentadas por estos materiales curriculares y de este modo llegar a conocer, por un lado, a qué tipos de problemas se enfrentan los alumnos en la escuela; por otro, cuáles son las prácticas educativas que estos materiales promueven, es decir, cuál es la verdadera función que desempeñan los problemas en los libros de texto. Este objetivo general se ha concretado de forma específica en la revisión de estudios que han analizado la frecuencia y variabilidad de las diferentes categorías y subcategorías de problemas de acuerdo con su estructura semántica en los libros de texto de diferentes sistemas educativos. Tras la revisión, hemos podido comprobar que la gran mayoría de los pav incluidos en los libros de texto se caracterizan fundamentalmente por una alta frecuencia de problemas consistentes (los más fáciles de resolver) y una reducida variabilidad de las distintas categorías y subcategorías de problemas. En consecuencia, estos problemas pueden resolverse aplicando estrategias superficiales, que, de acuerdo con Chamoso et al. (2014), acaban siendo automatizadas por los alumnos y no les serán de utilidad a la hora de enfrentarse con problemas con mayor nivel de dificultad. En palabras de Vicente et al. (2018), dada la simplicidad de los pav presentados en los libros de texto “difícilmente podrían considerarse herramientas eficaces para que los alumnos aprendan a resolver cualquier tipo de pav” (p. 100). Por otro lado, tal y como señalan Orrantia et al. (2005), una parte considerable de los pav se aproxima más a la función de un ejercicio que a la función de un verdadero problema. Los problemas se supeditan a la ejercitación de las operaciones aritméticas que los alumnos están estudiando en ese momento, de manera que la tendencia por parte de los libros de textos a considerar los problemas como un mero ejercicio rutinario al servicio de las operaciones de cálculo provoca que se desvirtúe la verdadera función de los problemas. Sin embargo, los problemas deberían constituir un fin en sí mismos, puesto que, como argumentan estos autores, el conocimiento conceptual desempeña un papel relevante en el proceso de rp, y este tipo de conocimiento se desarrolla en el propio proceso de resolución. Como hemos visto, esta misma idea es compartida por Chamoso et al. (2014) y por Despina y Harikleia (2014), para quienes es posible que la comprensión matemática de las diversas situaciones problemáticas se vea afectada debido a la escasa frecuencia de problemas con distintos niveles de dificultad y a la escasa variabilidad de problemas que ofrecen los libros de texto. En otro orden de ideas, los estudios de Chamoso et al. (2014), Vicente et al. (2018) y Tárraga et al. (2021) constatan que en España no ha habido evolución alguna con respecto al panorama presentado en el estudio precedente de Orrantia et al. (2005). En este sentido, Vicente et al. (2018) apuntan que “los libros de texto parecen mostrarse ajenos a las sucesivas reformas educativas realizadas en nuestro país” (p. 100). Según estos autores, llevar a cabo reformas educativas que eluden las cuestiones más cercanas a la práctica educativa puede limitar el aprendizaje de los alumnos, puesto que estos materiales curriculares definen realmente lo que éstos aprenden. Igualmente, en el ámbito internacional, los estudios de Despina y Harikleia (2014) y Tarim
(2017) respaldan tanto los resultados como las conclusiones de las investigaciones precedentes realizadas en Turquía y en Malasia. En concreto, los resultados del estudio de Tarim (2017) son coincidentes con los obtenidos por Olkum y Toluk (2002). Este hecho evidencia que, transcurridos quince años, los libros de texto utilizados en las escuelas primarias turcas no parecen responder a una planificación sistemática donde se tengan en cuenta aspectos básicos como una presencia equilibrada de las diferentes categorías y subcategorías de pav. La conclusión fundamental de esta revisión de estudios es que los libros de texto que
empleamos actualmente en las escuelas no constituyen una herramienta efectiva desde el
punto de vista didáctico para la enseñanza de los pav. La tipología de problemas que se incluyen en estos materiales no abarca todo el espectro de problemas matemáticos, sino que se centra en los más sencillos de resolver, lo que puede derivar en una deficiente formación en uno de los pilares fundamentales de la educación matemática. Por ello, los docentes deben ser conscientes de las limitaciones de los libros de texto, material hegemónico utilizado en las aulas, y tomar medidas para compensar estas limitaciones, de manera que adquieran la competencia para diseñar sus propios problemas matemáticos de acuerdo con los estándares recomendados por los currículos oficiales, con la frecuencia de éstos, su nivel de variabilidad y la graduación de su dificultad. Apple, M. W. (1992). The text and cultural politics. Educational Researcher, 21(7), 4-11. https://doi.org/10.3102/0013189X021007004 Boesen, J., Helenius, O., Bergqvist, E., Bergqvist, T., Lithner, J., Palm, T. y Palmberg, B. (2014). Developing mathematical competence: From the intended to the enacted curriculum. The Journal of Mathematical Behavior, 33, 72-87. https://doi.org/10.1016/j.jmathb.2013.10.001 Brehmer, D., Ryve, A. y Van Steenbrugge, H. (2016). Problem solving in Swedish mathematics textbooks for upper secondary school. Scandinavian Journal of Educational Research, 60(6), 577-593. https://doi.org/10.1080/00313831.2015.1066427 Cai, J. y Jiang, C. (2017). An analysis of problem-posing tasks in Chinese and us elementary mathematics textbooks. International Journal of Science and Mathematics Education, 15(8), 1521-1540. https://doi.org/10.1007/s10763-016-9758-2 Carpenter, T. y Moser, J. (1983). The acquisition of addition and substraction concepts in grades one through three. Journal for Research in Mathematics Education 15(3), pp. 179-202. https://doi.org/10.2307/748348 Chamoso, J. M., Vicente, S., Manchado, E. y Múñez, D. (2014). Los problemas de matemáticas escolares de primaria, ¿son solo problemas para el aula? Cuadernos de Investigación y Formación en Educación Matemática, 12, 261-279. De Corte, E., Greer, B. y Verschaffel, L. (1996). Mathematics teaching and learning. En D. C. Berliner y R. C. Calfee (Eds.), Handbook of Educational Psychology (pp. 491-549). MacMillan. De Lange, J. (1995). Assessment: No change without problems. En T. A. Romberg (Ed.), Reform in school mathematics (pp. 87-172). suny Press. http://www.fi.uu.nl/publicaties/literatuur/1131.pdf Depaepe, F., De Corte, E. y Verschaffel, L. (2009). Analysis of the realistic nature of word problems in upper elementary mathematics education in Flanders. En L. Verschaffel, B. Greer, W. Van Dooren y S. Mukhopadhyay (Eds.), Words and worlds: Modeling verbal descriptions of situations (pp. 245-263). Sense Publishers. Despina, D. y Harikleia, L. (2014). Addition and subtraction word problems in Greek grade A and grade B mathematics textbooks: distribution and children’s understanding. International Journal for Mathematics Teaching and Learning, 8, 340-356. https://eric.ed.gov/?id=ej1032727 Escudero, J. M. (2015). Prólogo. En R. Rodríguez, E. Bruillard y M. Horsley (Eds.), Digital textbooks: What’s new? (pp. 4-6). Servizo de Publicacións da usc/iartem. Fuchs, E. y Bock, A. (2018). The Palgrave Handbook of Textbook Studies. Hanbooks. https://doi.org/10.1057/978-1-137-53142-1 Hansen, T. I. (2018). Textbook use. En E. Fuchs y A. Bock (Eds.), The Palgrave Handbook of Textbook Studies (pp. 369-398). Handbooks. https://doi.org/10.1057/978-1-137-53142-1_27 Heller J. I. y Greeno, J. G. (1978). Semantic processing in arithmetic word problem solving. Ponencia presentada en Midwestern Psychological Association Convention. Chicago. Horsley, M. y Sikorová, Z. (2014). Classroom teaching and learning resources: International comparisons from timss. A preliminary review. Orbis Scholae, 8(2), 43-60. Kolovou, A., Van den Heuvel-Panhuizen, M. y Bakker, A. (2009). Non-routine problem solving tasks in primary school mathematics textbooks. A needle in a haystack. Mediterranean Journal for Research in Mathematics Education, 8(2), 31-68. Lester, F. K. (2013). Thoughts about research on mathematical problem-solving instruction. The Mathematics Enthusiast, 10(1), 245-278. Lewis, A. B. y Mayer, R. E. (1987). Student’s miscomprehension of relational statements in arithmetic word problems. Journal of Educational Psychology, 79(4), 363-371. https://doi.org/10.1037/0022-0663.79.4.363 López, E. M., Guerrero, A. C., Carrillo, J. y Contreras, L. C. (2015). La resolución de problemas en los libros de texto: un instrumento para su análisis. Avances de Investigación en Educación Matemática, 8, 73-94. https://doi.org/10.35763/aiem.v1i8.122 Marchis, I. (2012). Non-routine problems in primary mathematics workbooks from Romania. Acta Didactica Napocensia, 5(3), 49-55. Monterrubio, M. C. y Ortega, T. (2012). Creación y aplicación de un modelo de valoración de textos escolares matemáticos en educación secundaria. Revista de Educación, 358, 471-496. Olkun, S. y Toluk, Z. (2002). Textbooks, word problems and student success on addition and subtraction. International Journal for Mathematics Teaching and Learning. https://www.researchgate.net/publication/27569540_Textbooks_Word_Problems_and_Student_Success_on_Addition_and_Subtraction Orrantia, J., González, B. y Vicente, S. (2005). Un análisis de los problemas aritméticos en los libros de texto de educación primaria. Infancia y aprendizaje, 28(4), 429-451. https://doi.org/10.1174/021037005774518929 Ozer, E. y Sezer, R. (2014). A comparative analysis of questions in American, Singaporean, and Turkish Mathematics textbooks based on the topics covered in 8th grade in Turkey. Educational Sciences: Theory and Practice, 14(1), 411-421. Ruiz, A. (2013). La reforma de la educación matemática en Costa Rica. Perspectiva de la praxis. Cuadernos de Investigación y Formación en Educación Matemática, 10, 1-111. Sarabia, A. e Iriarte, C. (2011). El aprendizaje de las matemáticas: ¿Qué actitudes, creencias y emociones despierta esta materia en los alumnos? eunsa. Singh, P. y Hoon, T. (2010). An analysis of addition and subtraction word problems in mathematics textbooks used in Malaysian primary school classrooms. Brunei International Journal of Science and Mathematics Education, 2(1), 68-85. https://doi.org/10.1207/s1532690xci0303_1 Tarim, K. (2017). Problem solving levels of elementary school students on mathematical word problems and the distribution of these problems in textbooks. Çukurova University. Faculty of Education Journal, 46(2), 639-648. https://doi.org/10.14812/cuefd.306025 Tárraga, R., Tarín, J. y Lacruz, I. (2021). Analysis of word problems in primary education mathematics textbooks in Spain. Mathematics, 9(17), 3-18. https://doi.org/10.3390/math9172123 Van Stiphout, I. M. (2011). The development of algebraic proficiency. [Tesis doctoral. Universidad Tecnológica de Eindhoven]. Van Zanten, M. y Van den Heuvel-Panhuizen, M. (2018). Opportunity to learn problem solving in Dutch primary school mathematics textbooks. zdm: The International Journal on Mathematics Education, 50(7), 827-838. https://doi.org/10.1007/s11858-018-0973-x Vincent, J. y Stacey, K. (2008). Do mathematics textbook cultivate shallow teaching? Applying the timss video study criteria to Australian eighth-grade mathematics textbooks. Mathematics Education Research Journal, 20(1), 82-107. https://doi.org/10.1007/bf03217470 Vicente, S., Manchado, E. y Verschaffel, L. (2018). Resolución de problemas aritméticos verbales. Un análisis de los libros de texto españoles. Cultura y Educación, 30(1), 87-104. https://doi.org/10.1080/11356405.2017.1421606 Wijaya, A., Van den Heuvel-Panhuizen, M. y Doorman, M. (2015). Opportunity-to-learn contextbased tasks provided by mathematics textbooks. Educational Studies in Mathematics, 89(1), 41-65. https://doi.org/10.1007/s10649-015-9595-1
orcid: 0000-0001-5833-305X/Julio.Tarin@uv.es
Departamento de Didáctica y Organización Escolar, Universidad de Valencia (uv), España
orcid: 0000-0002-4458-5763/Raul.Tarraga@uv.es
Departamento de Didáctica y Organización Escolar, Universidad de Valencia (uv), España
resumen
abstract
palabras clave
key words
Introducción
La estructura semántica
Figura 1
Estructura de un problema de cambio 1
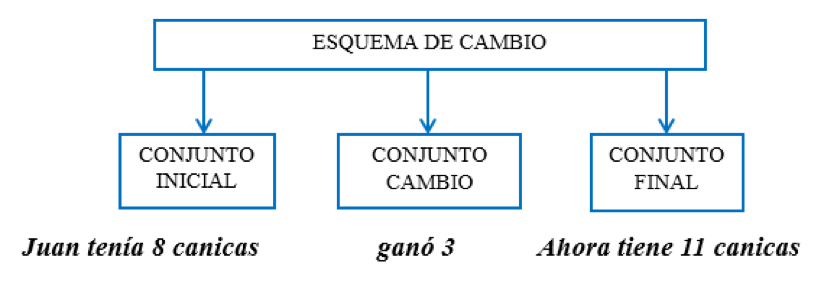
Fuente: Elaboración propia.
Metodología
Resultados
Tabla 1
Estudios sobre la estructura semántica de los problemas
Estudios
Tipos de problemas
Sistemas de categorización
Niveles
Editoriales analizadas
Orrantia et al. (2005)
pavea simples y compuestos
pavea combinados con pavempavea simples: Heller y Greeno (1978); Carpenter y Moser (1983)
pavea compuestos: sistema propuesto por los autores1.º-6.º ep
Santillana
Anaya
sm
Chamoso et al. (2014)
pavea simples y pavem
pav de estructura aditiva: Heller y Greeno (1978); Carpenter y Moser (1983)
1.º-6.º ep
Santillana
Despina y Harikleia (2014)
pavea simples
Van de Walle (1998)
1.º-2.º ep
Libros de texto y cuadernos complementarios (Ministerio de Educación griego)
Tarim (2017)
pavea simples
Van de Walle (1998)
1.º-3.º ep
Libros de texto y cuadernos complementarios (Ministerio de Educación turco)
Vicente et al. (2018)
pavea simples y pavem
Complejidad semánticomatemática en pavea: Riley y Greeno (1988)
Complejidad semánticomatemática en pavem: Greer (1992) y Vergnaud (1991)1.º-6.º ep
Santillana
sm
Tárraga et al. (2021)
pavea simples y compuestos
pavea combinados con pavempavea simples: Heller y Greeno (1978); Carpenter y Moser (1983)
pavea compuestos: sistema propuesto por Orrantia et al. (2005)1.º-6.º ep
Santillana
Anaya
smpavea: problemas aritméticos verbales de estructura aditiva
pav: problemas aritméticos verbales
pavem: problemas aritméticos verbales de estructura multiplicativa
ep: educación primariaConclusiones
Referencias