Aplicación de recocido simulado en problemas de optimización combinatoria
Jesús del Carmen Peralta Abarca, Jazmín Yanel Juárez Chávez, Beatriz Martínez Bahena
Facultad de Ciencias Químicas e Ingeniería (FCQeI), UAEM
Facultad de Contaduría, Administración e Informática (FCAeI), UAEM
Universidad Politécnica del Estado de Morelos (Upemor)
Desde hace ya mucho tiempo el ser humano, al descubrir el uso y la aplicación de la ciencia a su servicio, ha resuelto e intentado resolver muchos problemas a los cuales se enfrenta de manera cotidiana. Algunos de estos problemas son relativamente sencillos, pero también hay otros cuya solución no es tan fácil, y se ha querido encontrar una respuesta para facilitar tanto el trabajo como la vida.
Actualmente, existen problemas cuya resolución puede encontrarse dentro de las aplicaciones de la ingeniería. Moreno y colaboradores han identificado algunos de estos problemas: crear un plan de mínimo costo para repartir mercancías a clientes; realizar una asignación óptima de trabajadores a un conjunto de tareas; encontrar una secuencia óptima de trabajos en una cadena de producción; encontrar una distribución de tripulaciones de aviones con mínimo costo; encontrar la configuración óptima en una red de telecomunicaciones; crear un calendario de exámenes que minimice la probabilidad de traslapes, entre otros.1
Para tales casos es necesario que, al formular o plantear el modelo que los resuelva, este cumpla con las restricciones que tiene para minimizar o maximizar sus gastos o beneficios, según sea el caso. Esto es optimizar.
Los problemas anteriores se consideran problemas de optimización combinatoria, porque todos tienen las siguientes consideraciones: 1) existe un conjunto de objetos (clientes, tareas, trabajos, tripulaciones, exámenes, entre otros) que se han de colocar en distintas posiciones; 2) existe un grupo de lugares en los cuales se deben colocar dichos objetos.2 Cada colocación de objetos en un lugar determinado se denomina configuración.
La optimización combinatoria es una rama de la investigación de operaciones que se dedica al estudio de las configuraciones.3 Con ella se busca la mejor configuración, según sea el caso (maximizar o minimizar el valor requerido), para poder resolver un problema determinado.
Los problemas que aborda la optimización combinatoria son de una amplia diversidad, tanto en sus características como en sus variables, y lo que los hace diferentes. A veces no permite el uso de un mismo esquema de solución. Por ello se han diseñado varios métodos, en su mayoría “personalizados”, para solucionarlos.
Pero no todos los problemas que se presentan son sencillos, cada uno tiene su grado de dificultad. Una forma de determinar si un problema es fácil o difícil es a través del estudio de su complejidad algorítmica, la cual los clasifica de acuerdo con su complejidad computacional.
Según la teoría de la complejidad,4 los problemas se clasifican en:
Clase P. Existe una máquina de Turing determinista que los puede resolver en un tiempo polinómico, es decir, existe un algoritmo determinista con complejidad polinomial que los puede solucionar.
Clase NP. No existe una máquina de Turing determinista que pueda resolverlos en un tiempo polinómico. Estos problemas son aquellos cuya solución, hasta la fecha, no se ha encontrado de manera exacta por medio de algoritmos deterministas en tiempo polinomial.
Los problemas que se presentan en diversas áreas de la ingeniería se encuentran dentro de la clasificación NP, que son los más difíciles de resolver.5
Por lo anterior, en estos últimos años se ha registrado un crecimiento en el desarrollo y uso de métodos aproximados mediante procedimientos heurísticos para resolver problemas combinatorios. Este auge se debe a la necesidad de contar con herramientas y disponer de ellas para ofrecer soluciones rápidas a problemas reales. Estos procedimientos se conocen como técnicas heurísticas y metaheurísticas.
Técnicas heurísticas y metaheurísticas
Las heurísticas son algoritmos que encuentran soluciones de buena calidad para los problemas combinatorios complejos, mas no garantizan la optimalidad de la solución encontrada.6 Los algoritmos heurísticos son fáciles de implementar y encuentran buenas soluciones con esfuerzos computacionales relativamente pequeños (en un tiempo razonable), pero no garantizan encontrar la solución óptima global de un problema.
En problemas de gran tamaño, rara vez un algoritmo heurístico encuentra la solución óptima global. Una definición formal sería: “Es un procedimiento simple, a menudo basado en el sentido común, que se supone ofrecerá una buena solución (aunque no necesariamente la óptima) a problemas difíciles, de un modo fácil y rápido”.7
Por su parte, las metaheurísticas son estrategias de búsqueda inteligente diseñadas para mejorar procedimientos heurísticos. Aunque tampoco garantizan la obtención de un óptimo global, sí consideran, a diferencia de las heurísticas, mecanismos que les permiten escapar de óptimos locales,8 orientando la exploración de soluciones conforme se va dando el proceso de búsqueda.
En la figura 1 se muestra un esquema donde se aprecia la diferencia entre un óptimo local y un óptimo global.
Los cuatro procedimientos metaheurísticos más utilizados en la optimización combinatoria son recocido simulado; búsqueda tabú; GRASP, y algoritmos genéticos. En este artículo solo se hará referencia al primero.9
Recocido simulado
El recocido simulado se define como un método de búsqueda por entornos, caracterizado por un criterio de aceptación de soluciones vecinas —ver más adelante— que se adapta a lo largo de su ejecución. Es una de las metaheurísticas más aplicadas en optimización combinatoria e inclusive se ha combinado con otras estrategias heurísticas y metaheurísticas. Fue propuesto por Kirkpatrick, Gelatt y Vecchi en 1983, e inicialmente se creó para minimizar funciones de costo; pero también se utiliza ampliamente en problemas de maximización.
Asimismo, está inspirado en el proceso de recocido de sólidos, el cual utiliza un procedimiento que va disminuyendo la temperatura, con lo cual se modifica la estructura del material. El enfriamiento debe hacerse de manera lenta para obtener configuraciones moleculares resistentes. Cada etapa del enfriamiento tiene asociada una energía y una configuración del material determinadas (figura 2).
Metodología del recocido simulado
El pseudocódigo del recocido simulado se presenta en la figura 3.10 En él se muestran el bloque de búsqueda local (conocido como Ciclo de Metrópolis) y el “mecanismo de escape” (criterio de aceptación de Boltzmann).
El algoritmo comienza con una solución inicial (S0), para la cual se calcula el valor o costo f(S0) (lo que se quiere optimizar). A esta solución se le hacen modificaciones, conocidas como “perturbaciones”, en donde a la solución inicial (S0) se le cambia la configuración, obteniendo así una solución vecina11(S1) en las iteraciones sucesivas.
En cada iteración hay un conjunto de soluciones vecinas; cualquiera de ellas puede ser la nueva solución y es aceptada como buena si consigue reducir la función de costo. Al conjunto de soluciones vecinas (Sn) derivadas de una solución inicial se le conoce como “vecindad” o “entorno”, por el concepto de proximidad o vecindad entre las soluciones.
Figura 1. Diferencia entre óptimo local y global
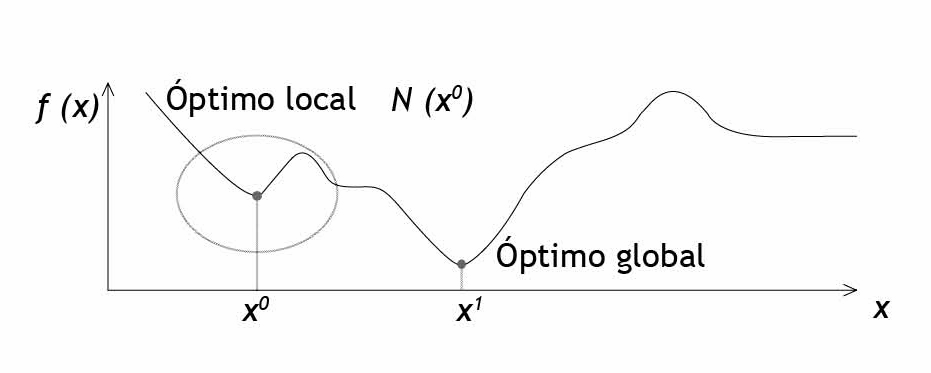
La intención es que cada vez que se modifique la solución, esta reduzca o maximice su costo para poder obtener una solución final optimizada; si el costo de la solución perturbada reduce el valor de la solución vecina, dicho costo se asigna a la solución inicial:
(So) (S)
Pero no siempre sucede así. Algunas soluciones vecinas tendrán un costo mayor que la solución anterior, por lo cual es necesario emplear un criterio de aceptación conocido como función de probabilidad de Boltzmann:
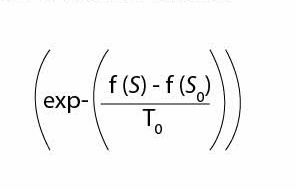
Esta función es aplicada para poder “escapar” de óptimos locales. Si se va a maximizar, se elimina el signo menos. La función trabaja de la forma siguiente: se obtiene un número aleatorio entre 0 y 1, y se calcula el valor de la función de Boltzmann. Si el valor del número aleatorio es mayor que el de Boltzmann, se desecha esa solución. En caso contrario, se acepta como una solución buena y este costo se le asigna a la solución inicial: (S0) = (S). Hacer esto permite buscar la solución del problema en otro espacio de soluciones.
Se sugiere revisar el pseudocódigo mostrado en la figura 3 para comprender mejor este paso, en la parte descrita como criterio de Boltzmann.
Mecanismo de enfriamiento
El algoritmo de mecanismo de enfriamiento12 repite su ciclo varias veces. Este número de repeticiones lo determina el usuario combinando los parámetros siguientes, que son parte importante en el algoritmo de recocido simulado y que forman parte de su mecanismo de enfriamiento, conocido así porque es la forma en la cual se puede emular con el proceso de solidificación de sólidos:
1. Parámetro de control inicial (comúnmente conocido como temperatura inicial T0). Dentro de los parámetros importantes para el buen funcionamiento del recocido simulado, la temperatura inicial tiene un papel clave. Este valor debe ser lo suficientemente alto para permitir que todos los cambios sean aceptados. Si T alcanza valores pequeños ya no habrá más movimientos.
2. Parámetro de control final (temperatura final Tf ). Es la condición de terminación del algoritmo.
3. Coeficiente de decremento de la temperatura (α); la temperatura va disminuyendo su valor conforme van dándose los ciclos hasta llegar al valor Tf .
4. Longitud de la cadena de Markov. Este número corresponde con el número de ciclos de Metrópolis.
Aplicaciones
La aplicación del recocido simulado es muy variada dentro de los campos de la ingeniería: en logística, producción, transporte, mecánica, electrónica, entre otros. Dentro de la Universidad Autónoma del Estado de Morelos (UAEM), específicamente en el posgrado de la Facultad de Ciencias Químicas e Ingeniería (FCQeI) y el Centro de Investigación en Ingeniería y Ciencias Aplicadas (Ciicap), en el área de optimización y software se han realizado investigaciones aplicando este algoritmo.
Figura 2. Configuraciones de un sólido aplicando recocido simulado

La metodología de trabajo es muy similar: se inicia con una propuesta de solución con un “costo inicial”, que puede ser determinado por unidades de tiempo, longitud, dinero, peso, distancias, entre otros, dependiendo del problema a tratar y del resultado esperado después de aplicar el algoritmo de recocido simulado. De ahí se obtiene una solución que maximiza o minimiza el costo de inicio. A continuación se presentan tres aplicaciones del recocido simulado en investigaciones desarrolladas en la UAEM:
1. En el área de materiales. El acero microaleado tiene una gran demanda en la industria aeroespacial y otras de alta tecnología. Debe cumplir con ciertas características en su composición química para ciertas aplicaciones y usos. Por tal motivo, es necesario diseñar y fabricar materiales con los requerimientos solicitados y probar si son adecuados para la función a realizar. Lo anterior implica desarrollar una amplia cantidad de configuraciones posibles que cumplan con las exigencias solicitadas.
Figura 3. Pseudocódigo del algoritmo de recocido simulado
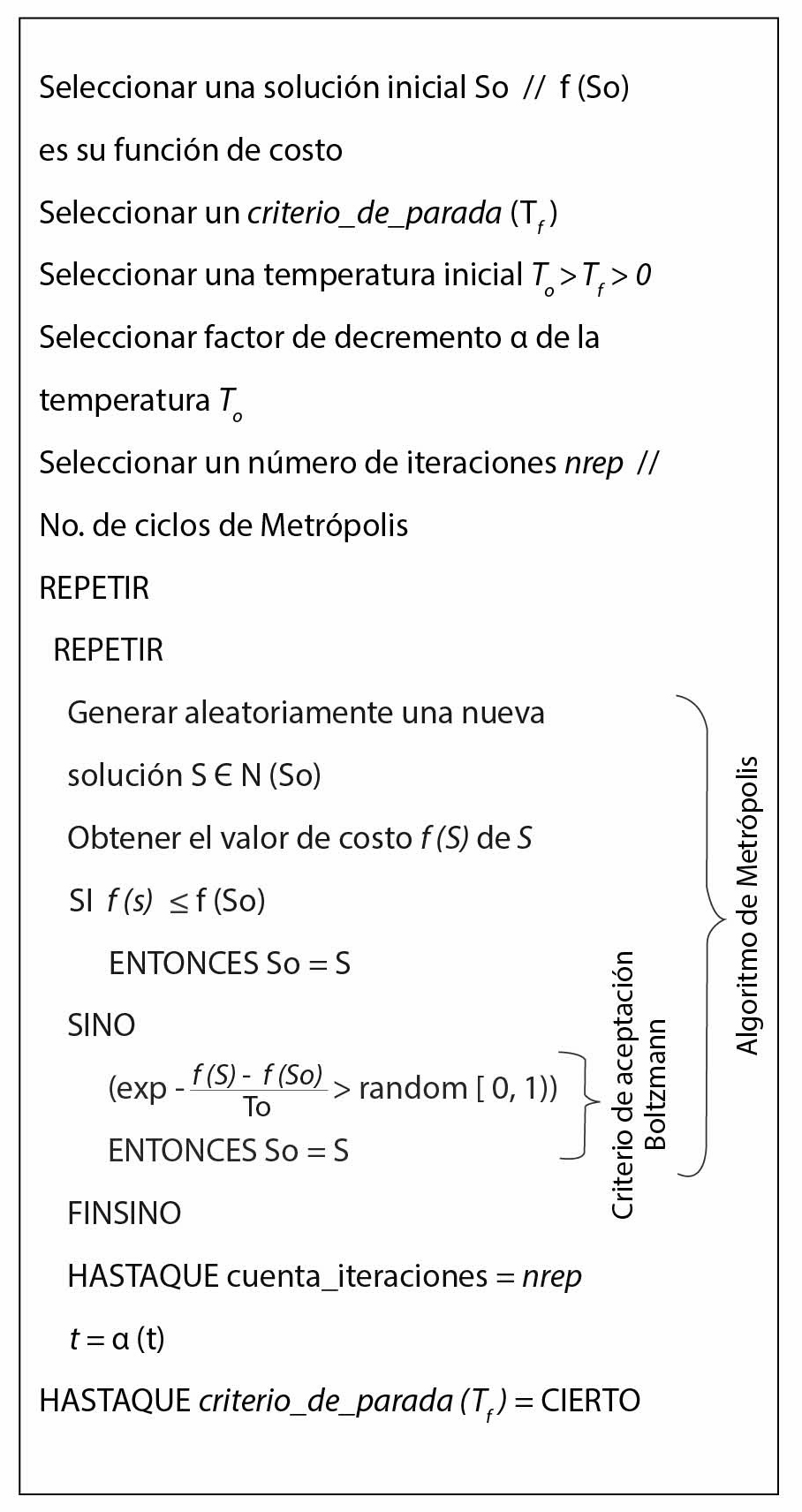
Para verificar si el material cumple con lo requerido, hay que realizar pruebas experimentales (con materiales de ensayo), lo cual resulta muy costoso por tratarse de pruebas de tipo destructivo.13
Una aplicación consiste en encontrar la mejor configuración de elementos de un acero microaleado, que ofrezca una mejor resistencia mecánica, es decir, maximizar dicha resistencia.14 Para esto, el recocido simulado recibe como parámetro de entrada (solución inicial) la composición química, el tamaño de grano y los precipitados, y devuelve una configuración con los valores que dan el mejor resultado en resistencia. La mejor solución encontrada fue la que se obtuvo. Para este caso, los valores más altos son de σ y MPa=562.1482, y los valores iniciales son de σ y MPa=0.
Al aplicar el algortimo se logra un ahorro en cuanto a reactivos y material empleado, porque se reduce el número de ensayos a realizar para obtener la configuración que cumpla con las características solicitadas por el cliente.
2. En el área de hidráulica. El problema del árbol de expansión mínima (formulado por Otakar Borukva en 1926) se aplica en diferentes áreas de redes, como las hidráulicas, eléctricas, de comunicaciones, entre otras, en las que se requiere minimizar costo, longitud, cantidades, distancia u otras medidas. Pero el diseño de una red hidráulica es muy costoso. Por ello es necesario aplicar métodos para encontrar posibles soluciones de forma eficiente. La aplicación del recocido simulado a este problema nos permite encontrar el mejor diseño con el costo mínimo.15
3. En el área de logística. El problema de ruteo vehicular es uno de los más utilizados y ha sido intensamente estudiado, debido a que tiene muchas aplicaciones prácticas en el campo de la logística.16 Consiste en un diseño óptimo de redes logísticas (rutas) para la entrega o recolección de bienes o personas desde un depósito central hacia un conjunto de puntos geográficamente dispersos, el cual está sujeto a varias limitaciones, como capacidad del vehículo, longitud de la ruta, horarios de carga y descarga, entrega o recolección, relaciones de precedencia entre los clientes, entre otras limitaciones.17
El planteamiento inicial del problema de la logística de distribución consiste en encontrar un plan de entrega de bienes/servicios a un conjunto de clientes geográficamente dispersos, minimizando el costo de recorrido de los vehículos.
Concluyendo, el algoritmo de recocido simulado tiene una vasta aplicación en muchos tipos de problemas de la vida real y es uno de los más utilizados con muy buenos resultados.
Notas
1 Pilar Moreno Díaz, Gabriel Huecas Fernández-Toribio, Jesús Sánchez Allende y Almudena García Manso, “Metaheurísticas de optimización combinatoria: uso de simulated annealing para un problema de calendarización”, Tecnologí@ y desarrollo. Revista de Ciencia, Tecnología y Medio Ambiente, vol. V, 2007, pp. 1-25.
2 Miguel Sánchez García, “Optimización combinatoria”, en Antonio Martinón Cejas (coord.), Las matemáticas del siglo XX, una mirada en 101 artículos, Universidad de La Laguna/Sociedad Canaria Isaac Newton de Profesores de Matemática/Nivola, San Cristóbal de la Laguna, 2000, pp.115-120.
3 Laurence A. Wosler y George L. Nemhauser, Integer and combinatorial optimization, Wiley & Sons, Nueva York, 1999.
4 Para más detales sobre su aplicación en optimización combinatoria, véase Marco Antonio Cruz Chávez, Pedro Moreno Bernal y Jesús del Carmen Peralta Abarca, “Aplicación de la teoría de la complejidad en optimización combinatoria”, Inventio, núm. 20, marzo-junio 2014, pp. 35-45,http://goo.gl/QDGTGt, consultado en febrero de 2015.
5 Michael R. Garey y David S. Johnson, Computers and intractability: a guide to the theory of NP completeness, W. H. Freeman & Co., Nueva York, 1979.
6 En optimización combinatoria se dice que una solución es buena cuando se acerca al valor óptimo (VO) de la solución. Un VO se obtiene cuando se “encuentran” los valores exactos de las variables que resuelven un problema. En cierto tipo de problemas no se conoce o no se sabe cuál es el VO; por esto se justifica el uso de las heurísticas como medio para encontrar una buena solución.
7 Stelios H. Zanakis y James R. Evans, “Heuristic ‘optimization’: why, when and how to use it”, Interfaces, vol. 11, núm. 5, 1981.
8 “Óptimos locales” son aquellas soluciones que ya no pueden ser mejoradas por el análisis actual, es decir, son los mejores valores encontrados en una determinada vecindad.
9 José M. Moreno y José A. Moreno, Heurísticas en optimización, Gobierno de Canarias/Consejería de Educación, Cultura y Deportes/Dirección General de Universidades e Investigación (Colección Textos Universitarios), Tenerife, 2000.
10 Emile L. Aarts y Jan K. Lenstra, Local search in combinatorial optimization, Princeton University Press, Nueva Jersey, 2003.
11 “Solución vecina” es el resultado de intercambiar elementos de una configuración inicial (S0) para obtener una nueva solución (S1).
12 Kathryn A. Dowsland y Belarmino Adenso Díaz, “Heuristic design and fundamentals of the simulated annealing”, Inteligencia Artificial. Revista Iberoamericana de Inteligencia Artificial, núm. 19, 2003, pp. 93-102, http://goo.gl/eTdI8T, consultado en febrero de 2015.
13 Las pruebas destructivas se distinguen por un muestreo y por la destrucción del producto para valorar el nivel de calidad del proceso desarrollado en él.
14 Jazmín Yanel Juárez Chávez, Algoritmo de recocido simulado para maximizar la resistencia mecánica en aceros microaleados, tesis de Maestría en Ingeniería y Ciencias Aplicadas, Ciicap, UAEM, 2011.
15 Beatriz Martínez Bahena, Solución del problema del árbol de expansión mínima aplicando recocido simulado con búsqueda tabú, tesis de Maestría en Ingeniería y Ciencias Aplicadas, Ciicap, Cuernavaca, 2011.
16 Petrica C. Pop, Corina Pop Sitar, Ioana Zelina, Vasile Lupse y Camelia Chira, “Heuristic algorithms for solving the generalized vehicle routing problem”, International Journal of Computers Communications & Control, vol. VI, núm. 1, marzo de 2011, pp. 158-165.
17 Gilbert Laporte, “The vehicle routing problem: an overview of exact and approximate algorithms”, European Journal of Operational Research, vol. 59, 1992, pp. 345-358