Esquema de enfriamiento en la metaheurística de recocido simulado

Jesús del Carmen Peralta-Abarca •
Juana Enriquez-Urbano ••
Beatriz Martínez-Bahena ••
Alfonso D'Granda-Trejo ••


Una de las metaheurísticas más utilizadas en optimización combinatoria, propuesta por Kirkpatrick, Gelat y Vechi,1 es la de recocido simulado (rs), la cual se considera como una técnica de búsqueda aleatoria. La metaheurística rs se basa en los principios de la mecánica estadística, que requiere en el proceso de recocido primero calentar y después enfriar lentamente un metal para obtener una estructura cristalina fuerte. Su funcionamiento se basa en un fenómeno físico relacionado con el comportamiento de los átomos (energía E) y los cambios de temperatura (T). En física, el enfriamiento demasiado rápido de un metal produce imperfecciones en su estructura; por el contrario, al enfriarse lentamente, los átomos tienen tiempo de asentarse en una red cristalina perfecta.2

La resistencia de la estructura depende de la velocidad de enfriamiento de los metales. Si la temperatura inicial no es suficientemente alta o se aplica un enfriamiento rápido se obtienen imperfecciones (estados metaestables).3 En este caso, el sólido enfriado no alcanzará el equilibrio térmico en cada temperatura. Los cristales fuertes se forman con un enfriamiento cuidadoso y lento. El algoritmo de rs simula los cambios de energía en un sistema sometido a un proceso de enfriamiento hasta que converge a un estado de equilibrio (estado congelado). Este esquema fue desarrollado en 1953 por Metrópolis y colaboradores, quienes modelaron en el proceso de rs los cambios energéticos en un sistema de partículas conforme decrece la temperatura hasta que converge en un estado estable.4

El uso del rs en optimización combinatoria se basa en establecer analogías entre el sistema físico y el problema de optimización. La tabla 1 muestra las analogías entre ambas partes.

El método rs traslada el proceso de recocido a la solución de un problema de optimización combinatoria. La función objetivo del problema,similar a la energía del material, es minimizada (o maximizada) con la ayuda de una temperatura, la cual es un parámetro de control del algoritmo. Éste debe tener el mismo efecto que la temperatura del sistema físico: conducir hacia el estado óptimo. La variable de temperatura se inicializa a un valor alto, denominado temperatura inicial 𝑇𝑇0, y se va reduciendo cada iteración mediante un mecanismo de enfriamiento ∝ de la temperatura hasta alcanzar una temperatura final 𝑇𝑇𝑓𝑓. Si este parámetro de la temperatura se disminuye gradual y controladamente se puede alcanzar el mínimo global, pero si se disminuye de forma precipitada se puede llegar a un mínimo local.

Tabla 1
Analogía entre sistema físico y problema de optimización

Sistema físico (termodinámica) Problema de optimización
Estados del sistema
Energía
Cambio de estado
Temperatura
Metaestable
Estado estable		 Soluciones factibles
Función de costo (función objetivo)
Solución vecina
Parámetro de control T
Óptimo local
Óptimo global (solución óptima)

Considerando el estado 𝑠𝑠 como una solución posible del problema de optimización 𝑓𝑓(𝑠𝑠), que es la función evaluada con la posible solución, se toma 𝑠𝑠 como el costo del estado, se genera un nuevo estado 𝑠𝑠‘ (nueva solución), y 𝑓𝑓(𝑠𝑠‘) es el costo del estado 𝑠𝑠‘.

El Ciclo de Metrópolis es la característica esencial del rs y determina cómo explorar aleatoriamente nuevas soluciones, rechazándolas o aceptándolas para el parámetro de temperatura (𝑇𝑇) constante. Es decir, el proceso de movimiento de un estado al siguiente es repetido por un número de iteraciones en la misma temperatura hasta que se logre el equilibrio.

El criterio de Metrópolis evalúa la diferencia de energía (costo) de la solución actual (s) con respecto a la nueva solución. Para el caso de minimización, si ésta es menor o igual a cero, Δ𝐸𝐸 = 𝑓𝑓(𝑠𝑠’) − 𝑓𝑓(𝑠𝑠) y ΔE ≤0, se acepta la nueva solución. Si no se cumple esta condición, se aplica el criterio de aceptación de Boltzmann, donde la nueva solución es aceptada con una probabilidad P(ΔΕΕ), que muestra la ecuación 𝑃𝑃(Δ𝐸𝐸) = 𝑒𝑒−(Δ𝐸𝐸⁄𝑇𝑇) llamada probabilidad de aceptación de Boltzmann.5 Esto se realiza para evitar quedar atrapado en óptimos locales.6

Una parte importante del rs es la definición de los parámetros que van a permitir que el algoritmo logre un resultado óptimo para el problema. Son los siguientes:

Estos parámetros no dependen directamente del problema, pues no representan un sentido físico. Al aplicar el algoritmo de rs para resolver un problema definido es necesario adaptar cada uno de estos parámetros al problema por resolver.

Temperatura inicial. Si la temperatura inicial es muy alta, el algoritmo permite que muchas soluciones (s’) sean aceptadas aun cuando no ofrezcan una mejora en función del costo. Por otra parte, si la temperatura es baja puede caer en óptimos locales con mayor facilidad. Por lo tanto, se debe tener un balance al momento de inicializar este parámetro. Se puede comenzar ejecutando el algoritmo con un número corto en cuanto a la longitud de la Cadena de Markov para observar la tasa de aceptación (criterio de aceptación de Boltzmann). Si esta tasa es convenientemente alta, la temperatura con la cual se experimentó puede usarse como el valor inicial T0.

El significado de “convenientemente alta” varía de un problema a otro; pero en muchos casos, si esta temperatura tiene un porcentaje de aceptación de Boltzmann de todas las soluciones (s’) generadas entre 90% y 95% (gráfica), se considera aceptable porque su probabilidad es cercana a 1, lo cual indica que es una temperatura adecuada.8 Inicialmente se acepta un alto porcentaje de soluciones malas, lo que permite la exploración del espacio de soluciones.

Mecanismo de enfriamiento. Se refiere a la forma en que la temperatura inicial va reduciéndose (𝑇𝑇0 → 0) conforme avanza la búsqueda para el caso de minimización, y se determina la velocidad de disminución de la temperatura a medida que avanzan las iteraciones del algoritmo.9 Existen diferentes maneras de abordar el decrecimiento de la temperatura. Una de las más utilizadas debido a su simplicidad y a los buenos resultados que ha dado en numerosas aplicaciones es la forma exponencial o geométrica. La ecuación de decremento de temperatura geométrica es 𝑡𝑡𝑘𝑘+1 = 𝛼𝛼𝑡𝑡𝑘𝑘.

Donde tk+1 es la temperatura en la iteración k+1, tk es la temperatura en la iteración k y α es una constante cercana a 1, escogida en el rango de 0.85 a 0.99, valores propuestos y utilizados por Kirkpatrick.10 Otros algoritmos de enfriamiento utilizados son los siguientes:

Existen otras formas funcionales en el programa de enfriamiento que se pueden utilizar; sin embargo, no hay en la literatura recomendaciones concisas acerca de cuál es la mejor, pues esto depende del problema y, en ese caso, debe decidirse por experimentación. El proceso de enfriamiento, junto con la temperatura, permite realizar al principio un proceso de exploración con una alta aceptación de soluciones y, posteriormente, ir reduciéndolas hasta lograr una solución optimizada.

Número de repeticiones (iteraciones) para alcanzar el equilibrio. El rs ejecuta cierto número de repeticiones en cada nivel de temperatura (T) para alcanzar el equilibrio. Esto permite generar un número determinado de soluciones vecinas en esa temperatura. Una vez alcanzado este estado, la temperatura se reduce y el proceso se repite. Un esquema obvio es mantener un número de repeticiones constante en cada temperatura o, alternativamente, éste se puede variar según desciende la temperatura, dedicando suficiente tiempo de búsqueda a temperaturas bajas para garantizar que se visita el óptimo local, es decir, que conforme disminuye la temperatura se aumenta el número de repeticiones.12

Este parámetro indica el número de soluciones propuestas para una temperatura T. Lo que se pretende es lograr la convergencia del algoritmo para que, al realizar un número de repeticiones, las soluciones obtenidas terminen por aproximarse cada vez más al valor buscado. En la medida que el algoritmo requiera de un menor número de repeticiones para acercarse al valor numérico deseado se dice que tiene una mayor rapidez de convergencia. Si no se selecciona el número adecuado de repeticiones se corre el riesgo de no converger y alejarse cada vez más del resultado deseado.

Longitud de la cadena de Markov. La Cadena de Markov en rs está formada por el conjunto de transiciones de soluciones visitadas en cada temperatura para alcanzar un estado de equilibrio, es decir, es el número de repeticiones entre soluciones visitadas en una vecindad para una misma temperatura.

Temperatura final. Lo ideal, teóricamente, es que la temperatura debería reducirse hasta cero porque esto permite que el porcentaje de las soluciones (s’) generadas que no cumplen con el procedimiento de optimización (maximizar o minimizar) sean rechazadas. El criterio de Boltzmann reduce la probabilidad de aceptar soluciones malas cuando la temperatura tiende a cero.

Tabla 2
Comportamiento del criterio de aceptación de Boltzmann en un rango de temperatura T (20-0.001)

Número de repeticiones (iteraciones) Total de soluciones generadas Soluciones “malas” Soluciones “buenas”      a    % de aceptación de Boltzmann
1
 17779
 17456
 323
 -->
 98.18
1
 17974
 17647
 327
 -->
 98.18
3
 17766
 17407
 359
 -->
 97.98
4
 17796
 17433
 363
 -->
 97.96
5
 17947
 17563
 384
 -->
 97.86
...
 ...
 ...
 ...
 -->
 ...
486
 28633
 252
 28381
 -->
 0.88
487
 28493
 238
 28255
 -->
 0.84
488
 28596
 251
 28345
 -->
 0.88
489
 28562
 232
 28330
 -->
 0.81
490
 28480
 216
 28264
 -->
 0.76

Por lo general, la búsqueda converge hacia el óptimo local final antes de llegar a cero, tratar de alcanzar una temperatura cero puede ocasionar que el tiempo de ejecución del algoritmo crezca considerablemente. También se puede detener la ejecución del algoritmo cuando se haya producido un número determinado de iteraciones sin tener ya una solución aceptada. Dréo y colaboradores sugieren que se debe terminar el algoritmo después de tres etapas sucesivas de temperatura sin que haya ocurrido alguna aceptación.13

La forma en que trabaja el mecanismo de enfriamiento con respecto al parámetro de control de la temperatura se presenta en la tabla 2 y en la gráfica.

Como se observa en la gráfica, utilizando el mecanismo de enfriamiento de Kirkpatrick para el decremento del parámetro de temperatura (evaluada en la ecuación de t_(k+1)=αt_k) y generando un número de repeticiones suficientes (lcm) en cada temperatura se puede alcanzar la solución óptima, pues conforme hay un decremento de este parámetro (T) el algoritmo explora nuevas y mejores soluciones hasta alcanzar la convergencia. Cabe señalar que la velocidad de convergencia del algoritmo está determinada por el número de repeticiones (lcm) y la temperatura (T). Estos parámetros son evaluados a través del algoritmo de rs y la gráfica muestra los resultados obtenidos.

Gráfica
Porcentaje de aceptación de Boltzmann en un rango de temperatura T (20-0.001)

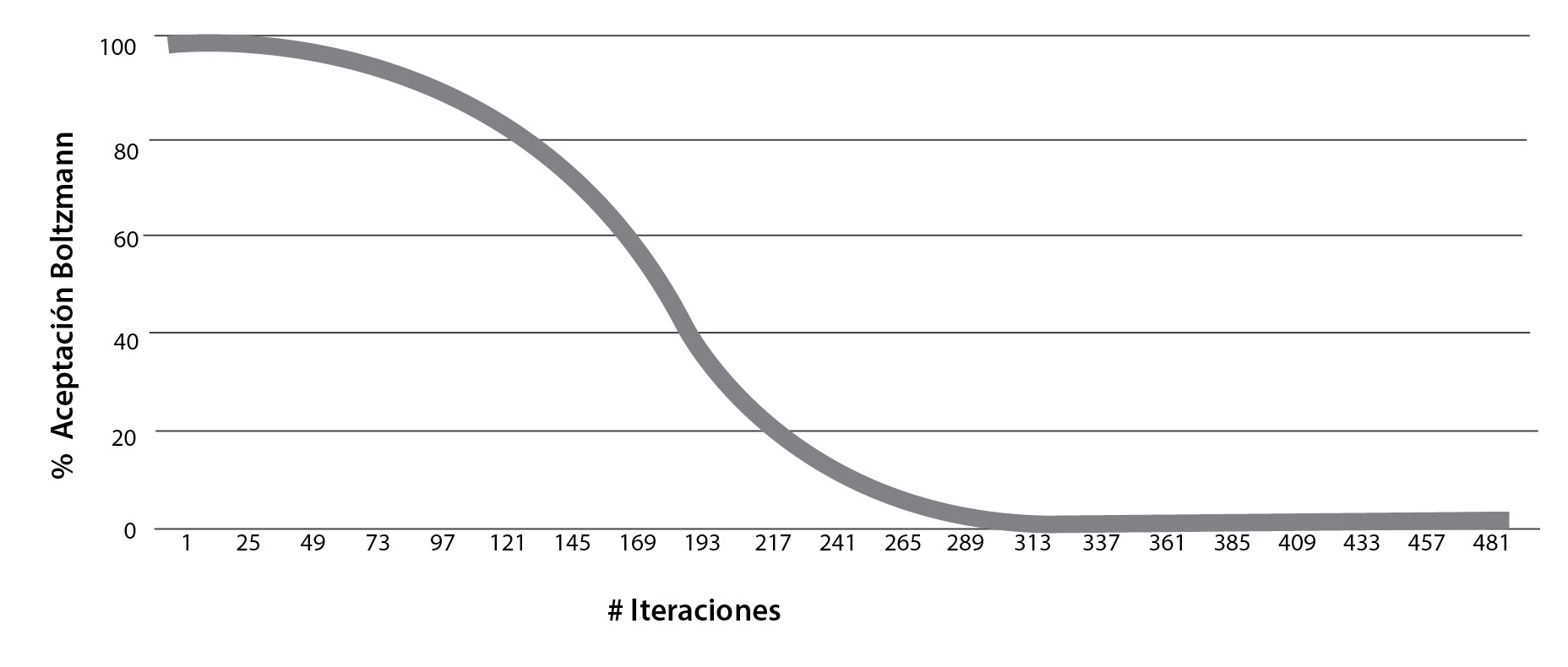
Dependiendo de los valores elegidos para los parámetros, las soluciones que se van encontrando pueden ser poco estables, esto es, van saltando mucho de unas a otras sin encontrar una solución buena con la rapidez suficiente. Lo anterior obliga a ajustar los parámetros en cada ejecución del algoritmo hasta lograr que los valores asignados permitan llegar al equilibrio térmico y a una solución estable. Esto conlleva un análisis de sensibilidad de los parámetros de control, que es un componente importante en la construcción de modelos matemáticos, computacionales y de simulación.14 El análisis de sensibilidad puede ser utilizado con simulación numérica para estudiar el comportamiento de un algoritmo.

La finalidad de este análisis es encontrar la mejor sintonización de los parámetros de control del algoritmo, de manera que éste tenga un mejor desempeño.

Existen otros elementos que también contribuyen en la convergencia del algoritmo, los cuales son dependientes de problema: el espacio de soluciones (S), la estructura de vecindad (S’), la función de costo (f(s)) y la solución inicial (s0).



• Profesora-Investigadora, Facultad de Ciencias Químicas e Ingenieria (FCQEI), Universidad Autónoma del Estado de Morelos (UAEM)

•• Profesor de tiempo parcial, FCQEI, UAEM/Estudiante del Doctorado en Ingenieria y Ciencias Aplicadas, Centro de Investigación en Ingeniería y Ciencias Aplicas (CIICAP)

Notas

1 Scott Kirkpatrick, C.D. Gelatt Jr. y M.P. Vecchi, “Optimization by simulated annealing”, Science, New Series, vol. 220, núm. 4598, 1983, pp. 671-680, doi: 10.1126/science.220.4598.671

2 Una explicación amplia de la metaheurística se encuentra en Jesús del Carmen Peralta-Abarca, Jazmín Yanel Juárez-Chávez y Beatriz Martínez-Bahena, “Aplicaciones de recocido simulado en problemas de optimización combinatoria”, Inventio, año 11, núm. 23, 2015, pp. 23-28, http://goo.gl/ax48Fz

3 En física, un estado metaestable es un mínimo local de energía que no es totalmente estable bajo perturbaciones del sistema por encima de cierta magnitud. Por eso se establece cierta magnitud o aceptación para considerar que pudo haber alcanzado cierta estabilidad y que, bajo ese criterio, ya no va a haber algo mejor.

4 Nacima Labadie, Christian Prins y Caroline Prodhon, Metaheuristics for vehicle routing problems, vol. 3, iSTE/John Wiley & Sons (Computer Engineering Series: Metaheuristic Set), Londres/Hoboken, 2016, pp. 39-40, doi: 10.1002/9781119136767

5 Jeffry Chavarría Molina y Juan José Fallas Monge, “Modelos de enfriamiento en recocido simulado”, Revista Digital. Matemática, Educación e Internet, vol. 16, núm. 2, 2016, doi: 10.18845/rdmei.v16i2

6 Los óptimos locales son soluciones que se refieren a mínimos o máximos locales, pero no son los mejores.

7 Pilar Moreno Díaz, Gabriel Huecas Fernández-Toribio, Jesús Sánchez Allende y Almudena García Manso, “Metaheurísticas de optimización combinatoria: uso de simulated annealing para un problema de calendarización”, Tecnologí@ y Desarrollo. Revista de Ciencia, Tecnología y Medio Ambiente, vol. 5, 2007, https://goo.gl/CvEdBH

8 Kathryn A. Dowsland y Belarmino Adenso-Díaz, “Diseño de heurísticas y fundamentos del recocido simulado”, Inteligencia Artificial. Revista Iberoamericana de Inteligencia Artificial, vol. 7, núm. 19, 2003, pp. 93-102, https://goo.gl/p254DD; Victor J. Rayward-Smith, I.H. Osman, C.R. Reeves y G.D. Smith (eds.), Modern heuristic search methods, John Wiley & Sons, Chichester, 1996, https://goo.gl/S5hoc5

9 Michele Gendreau, Gilbert Laporte y Jean-Yves Potvin, “Metaheuristics for the capaciteted vrp”, en Paolo Toth y Daniele Vigo (eds.), The vehicle routing problem, siam (Monographs on Discrete Mathematics and Applications), Filadelfia, 2002, pp. 129-154, doi: 10.1137/1.9780898718515

10 Scott Kirkpatrick et al., “Optimization…”, op. cit.

11 Pilar Moreno Díaz et al., “Metaheurísticas…”, op. cit.

12 Kathryn A. Dowsland y Belarmino Adenso-Díaz, “Diseño de heurísticas…”, op. cit.

13 Johann Dréo, Alain Pétrowski, Patrick Siarry y Eric Taillard, Metaheuristics for hard optimization: methods and case studies, Springer Verlag, Berlín, 2006, doi: 10.1007/3-540-30966-7

14 David J. Pannell, “Sensitivity analysis of normative economic models: theoretical framework and practical strategies”, Agricultural Economics, vol. 16, 2009, pp. 139-152, https://goo.gl/wQtbGi