Metaheurísticas

Jesús del Carmen Peralta-Abarca ^•
Pedro Moreno-Bernal ^••
Sergio Nesmachnow ^•••
Alfonso D’Granda-Trejo ^••••

Cuando surgió la disciplina de la Inteligencia Artificial (ia) en la década de 1950, los científicos en computación se propusieron concebir métodos para que las computadoras se comportaran de manera inteligente, es decir, que fuesen capaces de realizar tareas complejas con habilidad y eficiencia similar o superior a las que consigue un ser humano.¹

En 1976 Newell y Simon formularon la hipótesis del sistema de símbolos físicos. La idea principal de este postulado es que cualquier sistema, humano o artificial, que exhiba un comportamiento inteligente, debe operar manipulando estructuras de datos compuestas por símbolos.² Esta hipótesis sentó las bases para la creación de estrategias para resolver distintos tipos de problemas mediante técnicas computacionales.

Las primeras técnicas computacionales se basaron en mecanismos simples para resolver problemas sencillos. Inicialmente se pensaba que para resolver casos más complejos o de mayor dimensión era suficiente con incrementar las capacidades (velocidad, memoria, etc.) del hardware. Sin embargo, el desarrollo de la teoría de la complejidad computacional permitió identificar y caracterizar problemas para los cuales la resolución exacta de instancias realistas de gran dimensión demandaría cientos o miles de años, aun utilizando hardware de gran potencia.³

Durante los inicios de la investigación en ia, la resolución de problemas se centró en desarrollar mecanismos de búsqueda de propósito general, combinando elementos básicos para encontrar soluciones completas. Sin embargo, este enfoque no era apropiado para tratar problemas complejos. Como alternativa a las técnicas de búsqueda generales, se idearon métodos que incorporan conocimiento específico del dominio del problema. Mediante la aplicación de operaciones específicas, estos métodos permiten delimitar el espacio de búsqueda de soluciones de un problema, para resolver casos concretos en dominios de conocimiento restringido.⁴

Dada la necesidad de explorar una amplia variedad de problemas utilizando ia, surgieron los sistemas basados en el conocimiento, conocidos como sistemas expertos, introducidos por Feigenbaum en 1971, quien los define como “un programa inteligente para computadora que utiliza conocimiento y procedimientos inferenciales en la resolución de problemas suficientemente difíciles como para que su solución requiera una experiencia humana importante”.⁵ Según Feigenbaum, el conocimiento de un sistema experto está compuesto por hechos y por heurísticos. Los hechos constituyen un cuerpo de información sobre el cual existe consenso sobre su validez por parte de los expertos en el área. Los heurísticos son reglas intuitivas (reglas de razonamiento plausibles, conjeturas razonables) sobre las que se puede basar la toma de decisiones.⁶

En este contexto, el término heurístico hace referencia a un conjunto de reglas intuitivas, fundadas en conocimiento particular, para la toma de decisiones. Cada regla puede resolver una parte específica de un determinado problema, sin embargo, esa regla puede no resultar útil o funcional para resolver una situación particular en un problema diferente. Un método o regla heurística se guía por la intuición y por la experiencia, manifestando un conocimiento empírico y en general simulando un comportamiento humano.⁷

La búsqueda de soluciones

Un método de búsqueda es un procedimiento sistemático para hallar una solución a un determinado problema. Cuando existen múltiples soluciones candidatas, el procedimiento implica explorar el conjunto de posibles soluciones con el fin de identificar aquella(s) que proporcione(n) las mejores funcionalidades para resolver el problema en cuestión. Formalmente, el problema se puede formular mediante uno o varios objetivos, que son tomados en cuenta para evaluar las funcionalidades provistas por cada solución candidata, con el objetivo de hallar una que resuelva apropiadamente el problema.

Un mecanismo efectivo para resolver un determinado problema consiste en explorar todas y cada una de las soluciones candidatas. Se implementa de este modo una búsqueda exhaustiva del espacio de soluciones del problema. La búsqueda parte de un estado inicial caracterizado por una solución candidata y define un procedimiento sistemático para analizar y comparar todas las posibles soluciones. El procedimiento exhaustivo garantiza encontrar la solución de un problema (en caso de que exista) o determinar la inexistencia de una solución. Sin embargo, este tipo de métodos tienen un serio inconveniente que limita su aplicación en la práctica en problemas realistas: el número de pasos requeridos y por lo tanto también el costo computacional, en términos de tiempo de cómputo, para realizar la exploración completa del espacio de soluciones que puede ser muy grande, en especial al considerar problemas complejos y/o escenarios realistas de gran dimensión.

Para afrontar el problema del elevado costo computacional de los métodos de búsqueda exhaustiva se han propuesto métodos alternativos basados en realizar una exploración sistemática y más eficiente del espacio de soluciones. Los métodos denominados de búsqueda local se basan en un procedimiento que parte de una solución candidata inicial y que aplica una serie de pasos en los que iterativamente se explora un conjunto de soluciones vecinas, que difieren poco de la solución candidata que se considera en cada paso. Formalmente, a partir de una solución s, se define una estructura de vecindad N(s) como el conjunto que incluye todas las soluciones que pueden alcanzarse desde s mediante modificaciones simples o movimientos. Al explorar la vecindad de una solución s se compara cada elemento de la vecindad con s y se determina la solución que mejor resuelve el problema en cuestión, que pasa a ser la solución candidata a considerar en el siguiente paso del método.

El criterio utilizado para construir la vecindad determina las propiedades del método de búsqueda local. Es claro que un criterio demasiado exhaustivo puede conducir a una búsqueda poco eficiente computacionalmente, que se comportará como una búsqueda exhaustiva. En este contexto, los métodos heurísticos proporcionan criterios eficaces para definir búsquedas eficientes. La idea consiste en seleccionar para la comparación solamente aquellas soluciones promisorias, de la misma manera en que un experto aplicaría su intuición y experiencia, restringiendo la amplitud de la búsqueda para resolver un problema determinado. El procedimiento resultante es eficiente y efectivo para calcular soluciones de buena calidad, aunque no garantiza encontrar la solución óptima del problema.⁸

Considérese que se requiere encontrar la mejor solución de un problema, cuya calidad se puede evaluar mediante una función f(x), siendo x un conjunto de variables que definen o caracterizan a la solución s. En lugar de explorar todas las soluciones del espacio de búsqueda, es posible aplicar un procedimiento sistemático como el definido por el método de búsqueda local iterada (bli). Como se explicó previamente, el método bli parte de una solución inicial, que puede ser determinada aleatoriamente o seleccionada tomando en cuenta el conocimiento específico del problema. A partir de una solución candidata, bli aplica una búsqueda iterativa que consiste en reemplazar la solución actual por una mejor solución existente en su vecindad N(s), evaluada aplicando la función f(x). De este modo, la calidad de la solución mejora en cada iteración y el método es capaz de proporcionar una solución de alta calidad, inclusive puede alcanzar la solución óptima del problema. Dado que el método no necesariamente explora exhaustivamente todo el espacio de soluciones del problema, su desempeño (evaluado en uso de recursos computacionales y tiempo de ejecución) es muy superior a una búsqueda exhaustiva. Por este motivo, bli constituye una alternativa eficiente para la resolución de problemas.

El procedimiento definido por el método bli permite resolver exitosamente problemas con un único óptimo global, ya que la búsqueda iterada permite ‘subir la colina’ del óptimo y retornar esa solución. Sin embargo, el método no garantiza encontrar la mejor solución para problemas con óptimos locales, ya que la búsqueda iterada puede conducir a escalar la colina incorrecta (la del óptimo local) en lugar de la colina del óptimo global. Este comportamiento se ejemplifica en el diagrama presentado en la gráfica 1: el método bli permite resolver problemas con un único óptimo (problemas unimodales) pero puede fallar para problemas con más de un óptimo local (problemas multimodales).

Gráfica 1
Comportamiento del método bli en la resolución de problemas

a) función unimodal, el método es capaz de encontrar la solución óptima del problema, b) función multimodal, el método puede fallar en encontrar el óptimo global y retornar un óptimo local del problema.

Metaheurísticas

La palabra metaheurística se compone de dos términos griegos, “meta” (μετά) que significa más allá y “heurística” (ευρισκειν), que significa encontrar o descubrir. La palabra se utiliza para designar a procedimientos de resolución de problemas orientados a mejorar el desempeño y calidad de búsqueda proporcionados por las heurísticas. La primera mención al término ‘metaheurística’ fue realizada por Glover⁹ en el trabajo que definió las bases de este tipo de técnicas.

Las metaheurísticas se definen como procedimientos de búsqueda de alto nivel que aplican una regla heurística (o varias), que permite explorar el espacio de búsqueda de manera más eficiente que una búsqueda exhaustiva (en términos de tiempo y recursos computacionales requeridos) y de manera más eficaz que heurísticas simples (en términos de la calidad de las soluciones calculadas).

Para mejorar el procedimiento de búsqueda de los métodos heurísticos, las metaheurísticas proponen combinar diversos esquemas provistos por una serie de heurísticas subordinadas. De este modo, una metaheurística combina una o varias heurísticas con un procedimiento general de alto nivel que determina cómo coordinar la ejecución de las heurísticas subordinadas y proporciona mejoras al patrón de búsqueda.

Dos ejemplos relevantes de metaheurísticas que combinan una heurística de búsqueda local con un procedimiento de alto nivel para mejorar las capacidades de calcular buenas soluciones son Búsqueda Tabú (bt)¹⁰ y Recocido Simulado (rs).¹¹

rs se basa en potenciar a un método de búsqueda local iterada con un procedimiento que permite aceptar soluciones de peor calidad que la solución actual, con el propósito de escapar de óptimos locales. bt propone combinar una búsqueda local iterada con una memoria de corto plazo que guía la búsqueda; las soluciones examinadas en el pasado se incluyen en una lista tabú, prohibiendo que sean visitadas en los siguientes pasos de la iteración para evitar ciclos y escapar de óptimos locales.

Los dos casos presentados previamente ejemplifican claramente los objetivos concretos de las metaheurísticas: encontrar de manera eficiente soluciones de buena calidad y analizar el espacio de búsqueda, evitando quedar atrapadas en zonas específicas.¹² Dos conceptos relevantes se asocian con los objetivos mencionados: la exploración (o diversificación) del espacio de búsqueda y la explotación (o intensificación) de buenas soluciones encontradas previamente. La gráfica 2 ilustra estos conceptos, presentando los patrones exploratorios y de explotación que deben formar parte de la propuesta conceptual de toda metaheurística.

Gráfica 2
Patrón de búsqueda de una metaheurística

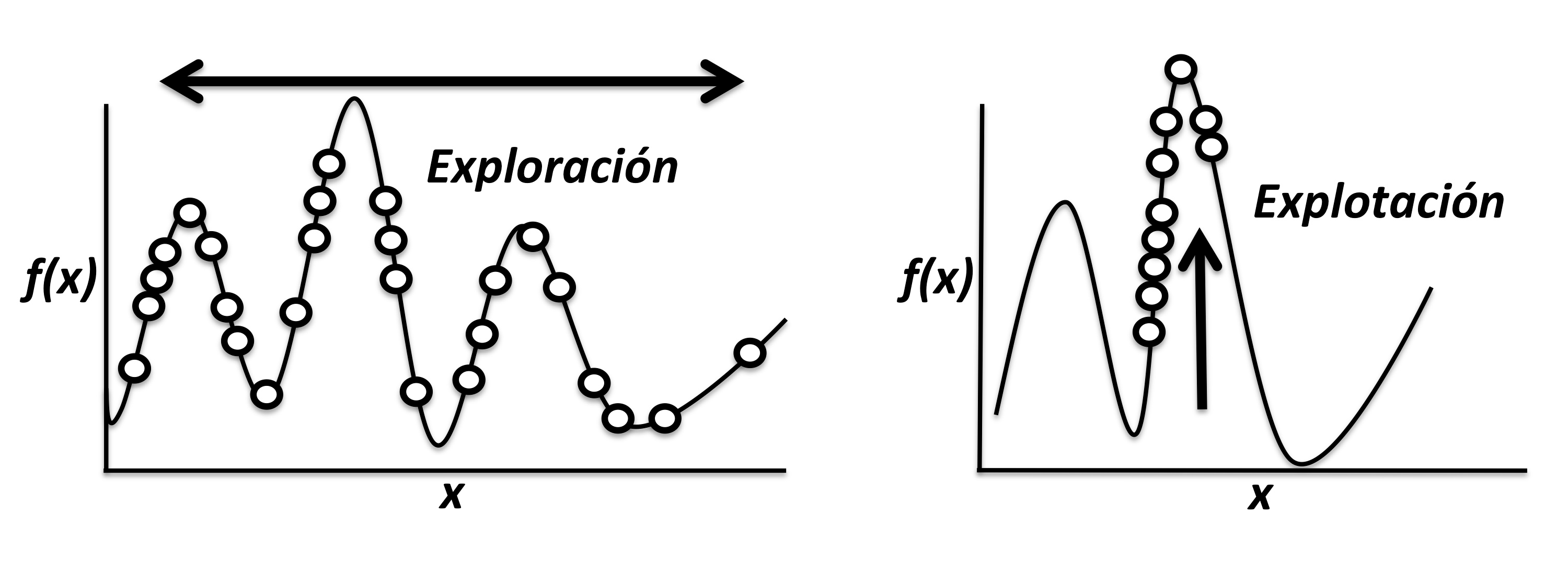
Conceptos vinculados con el patrón de búsqueda de una metaheurística: a) exploración del espacio de soluciones y b) explotación de buenas soluciones encontradas.

Los procedimientos que definen a las metaheurísticas suelen basarse en la emulación de conceptos y procesos bien conocidos y de validez intuitiva.

De este modo se han propuesto metaheurísticas basadas en procesos naturales como el enfriamiento de los metales (Recocido Simulado), la evolución natural (Algoritmos Evolutivos), el comportamiento social de insectos y aves (Optimización por Colonia de Hormigas y Optimización por Enjambre de Partículas) y otros fenómenos.

Tipos de metaheurísticas

Existen diversos criterios para clasificar a las técnicas metaheurísticas. Uno de los criterios más utilizados por la comunidad científica toma en cuenta el número de soluciones candidatas exploradas en cada paso de iteración. De acuerdo a este criterio, las metaheurísticas se clasifican en basadas en trayectoria, que manejan una única solución en cada paso de iteración, y basadas en población, que manejan un conjunto de soluciones candidatas en cada paso.¹³

Las metaheurísticas basadas en trayectoria reemplazan la solución candidata en cada paso, definiendo de esta manera una trayectoria en el espacio de búsqueda. Ejemplos conocidos de esta categoría son la Búsqueda Tabú, Recocido Simulado, Búsqueda Ávida Aleatoria Adaptativa (grasp por sus siglas en inglés), entre otras. Estos métodos son eficientes, al manejar solamente una solución en cada paso, pero pueden tener problemas para escapar de óptimos locales fuertemente atractivos.

Las metaheurísticas basadas en población utilizan un conjunto de soluciones candidatas en cada paso (la población). Un número determinado de soluciones se reemplazan en cada iteración por nuevas soluciones que se pueden construir por recombinación de otras soluciones en la población o por recombinación de un mecanismo exclusivo de las metaheurísticas basadas en población y consiste en construir nuevas soluciones a partir de la combinación de características de soluciones seleccionadas de acuerdo a su capacidad de resolver el problema en cuestión.

La mayoría de las metaheurísticas basadas en población son bioinspiradas. Los mecanismos para seleccionar y recombinar soluciones se basan en conceptos biológicos como la evolución natural, la sinergia e inteligencia colectiva de grupos de animales (hormigas, aves, abejas, murciélagos, etc.) u otros fenómenos similares. Ejemplos conocidos de esta categoría de metaheurísticas son Algoritmos Evolutivos, Optimización por Colonia de Hormigas, Optimización por Enjambre de Partículas, entre otras.

Los Algoritmos Evolutivos (ae) engloban a un conjunto de metaheurísticas muy populares y difundidas en los últimos treinta años, por su versatilidad para resolver un gran número de problemas. Los ae basan su funcionamiento en una emulación del proceso de evolución natural de los seres vivos, aplicando los conceptos neo-darwinistas de selección natural, supervivencia de los individuos más aptos y diversidad genética para resolver problemas de búsqueda, optimización y aprendizaje.¹⁴

Dentro de la categoría de los ae se engloban técnicas como los Algoritmos Genéticos, la Programación Genética, las Estrategias de Evolución, la Evolución Diferencial y otras.

El esquema de un ae se describe en Algoritmo 1. El ae aplica una búsqueda iterativa (cada iteración se denomina generación) sobre un conjunto de individuos (la población P). Cada individuo en la población representa una solución tentativa al problema a resolver. La calidad de cada solución representada se evalúa mediante una función de aptitud que determina qué tan adecuada es la solución para resolver el problema, de acuerdo a la(s) función(es) objetivo considerada(s). Inicialmente la población se genera de forma aleatoria o aplicando una heurística específica (y simple) para resolver el problema. En cada generación, el ae aplica probabilísticamente operadores de variación, como la recombinación de dos individuos y la aplicación de cambios aleatorios (mutación) en su contenido. La utilización de una técnica de selección de soluciones que emula a la selección natural, dando mayor posibilidad de supervivencia a los individuos más aptos (de acuerdo a sus valores de aptitud), conduce a la población del ae a soluciones de mejor calidad para el problema.

Algoritmo 1 Esquema de un Algoritmo Evolutivo      1   Inicialización de la población P      2   Mientras no se cumpla el criterio de parada      3   Evaluación de función de aptitud de P      4   Selección de los individuos más aptos      5   Recombinación de individuos      6   Mutación de individuos      7   Reemplazo de individuos, generando la nueva población      8   Fin mientras      9   Retorno del mejor individuo encontrado

El criterio de parada del ae usualmente involucra un número determinado de generaciones o un tiempo límite de ejecución, una cota de calidad en los valores de aptitud, o la detección de una condición de convergencia. Estrategias específicas se utilizan para seleccionar los individuos a recombinar (el operador de selección) y para determinar qué individuos se insertan en la población luego de aplicar los operadores evolutivos (el operador de reemplazo). Finalmente, el ae retorna el mejor individuo (solución) encontrado en el proceso, tomando en cuenta la función de aptitud considerada.

El mecanismo de búsqueda definido por un ae presenta un comportamiento robusto, tomando en cuenta la información presente en la población en cada generación y su capacidad de muestrear apropiadamente el espacio de búsqueda. Las múltiples variantes de operadores de recombinación y mutación existentes permiten definir diferentes balances entre la exploración y explotación del ae. Complementariamente, la capacidad de incluir información concreta sobre el problema a resolver, a través de representaciones u operadores específicamente diseñados proporcionan a los ae una gran versatilidad para la resolución de una amplia gama de problemas.

Aplicaciones

Las metaheurísticas han sido aplicadas exitosamente en múltiples áreas, en problemas académicos y del mundo real.

Entre las áreas de aplicación de mayor relevancia en ciencia, industria y comercio pueden destacarse:¹⁵

• Sistemas automáticos y de control: las metaheurísticas se han aplicado como métodos eficientes de aprendizaje para reducir la necesidad de la presencia humana en tareas automatizables.
• Bioinformática: las metaheurísticas se han posicionado como métodos eficaces para resolver problemas complejos que manejan grandes volúmenes de datos para el estudio de estructura de proteínas, diseño de fármacos, alineamiento de secuencias y otros problemas relevantes.
• Ingeniería: las metaheurísticas se han utilizado como métodos útiles para el diseño de sistemas con muchos componentes y funciones complejas como el diseño y optimización de perfiles aerodinámicos, procesamiento de señales e imágenes, diseño de maquinarias, electrónica, redes hidráulicas y otros problemas.
• Procesamiento de información: las metaheurísticas son métodos útiles para resolver problemas de selección de características, clasificación y agrupamiento de datos, procesamiento de lenguaje natural y otros.
• Manufactura e industria: las metaheurísticas permiten mejorar la competitividad en problemas relevantes de la economía globalizada, incluyendo optimización de líneas de ensamblaje y empaquetado, optimización de grandes almacenes, etc.
• Planificación y calendarización: las metaheurísticas impactan positivamente en la productividad y calidad de servicio, al utilizarse como ayuda a la toma de decisiones sobre la asignación de recursos a tareas importantes, en tiempos de ejecución reducidos.
• Ruteo y logística: las metaheurísticas son métodos útiles para manejar y optimizar el flujo de recursos en escenarios complejos de grandes dimensiones.
• Telecomunicaciones: las metaheurísticas permiten afrontar exitosamente problemas vinculados con el diseño y optimización de redes cableadas, inalámbricas y móviles.

Las metaheurísticas también se han aplicado exitosamente en otras áreas, incluyendo eficiencia energética, aplicaciones militares y de defensa, economía y finanzas, entre otras.

^• Profesora-investigadora, Facultad de Ciencias Químicas e Ingeniería (fcqei), Universidad Autónoma del Estado de Morelos (uaem)
^•• Profesor, Facultad de Contaduría, Administración e Informática (fcaei), uaem
^••• Profesor de tiempo completo, Universidad de la República
^•••• Profesor, fcaei, uaem

Notas

¹ Stuart Russell y Peter Norvig, Inteligencia artificial. Un enfoque moderno, Pearson Prentice Hall, Madrid, 2004, p. 21, https://bit.ly/2Go1mhB

² Idem.

³ Ibid., p. 25.

⁴ David Masip Rodó, Gerard Escudero Bakx, Raúl Benítez Iglésias, Samir Kanaan Izquierdo, Inteligencia artificial avanzada, Editorial uoc, Barcelona, 2014, p. 11, https://bit.ly/2VXJhzJ

⁵ Paul Harmon y David King, Sistemas expertos: aplicaciones de la inteligencia artificial en la actividad empresarial, Ediciones Díaz de Santos, Madrid, 1988, p. 5, https://bit.ly/2HhdWo6

⁶ David Masip Rodó et al., Inteligencia…, op. cit.

⁷ Stuart Russell y Peter Norvig, Inteligencia artificial…, op. cit.

⁸ Carlos Coello Coello, Gary B. Lamont y David A. van Veldhuizen, Evolutionary algorithms for solving multi-objective problems, Springer, Nueva York, 2007, https://bit.ly/2Cp1FZd

⁹ Fred Glover, “Future paths for integer programming and links to artificial intelligence”, Computers & Operations Research, vol. 13, núm. 5, 1986, pp. 533-549, doi: 10.1016/0305-0548(86)90048-1

¹⁰ Idem.

¹¹ Scott Kirkpatrick, Daniel C. Gelatt y Mario P. Vecchi, “Optimization by simulated annealing”, Science, vol. 220, núm. 4598, 1983, pp. 671-680, doi: 10.1126/science.220.4598.671

¹² Sergio Nesmachnow, “An overview of metaheuristics: accurate and efficient methods for optimization”, International Journal of Metaheuristics, vol. 3, núm. 4, 2014, pp. 320-347, doi: 10.1504/IJMHEUR.2014.068914

¹³ El-Ghazali Talbi, Metaheuristics: from design to implementation, John Wiley & Sons, Hoboken, 2009, https://bit.ly/2HfvQHZ

¹⁴ David E. Goldberg, Genetic algorithms in search, optimization & machine learning, Addison-Wesly Publishing Co., Boston, 1989, p. 25, https://bit.ly/2siPM1R

¹⁵ Xin-She Yang, Engineering optimization: an introduction with metaheuristic applications, John Wiley & Sons, Hoboken, 2010, doi: 10.1002/9780470640425; Shubhabrata Datta, Materials design using computational intelligence techniques, crc Press, Boca Raton, 2016, https://bit.ly/2HhOCyp; Olympia Roeva, Real-world applications of genetic algorithms, InTech, Londres, 2012, doi: 10.5772/2674